9.2 KiB
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра Микрорадиоэлектроники и технологии радиоаппаратуры
(МИТ)
ОТЧЕТ
по ИДЗ
по дисциплине «ОЭиР»
Тема: Исследование контактных явлений в структуре металл-полупроводник
Вариант 14,6,3
https://www.meme-arsenal.com/memes/4598e00877a721c55a46dc4aafb78719.jpg
Студент гр. 1181 Шишков Д.А. Преподаватель Филипюк И.А
Санкт-Петербург
2023
Задание:
Для заданной пары металл-полупроводник оценить кинетические свойства заданных материалов, рассчитать и построить энергетическую диаграмму и вольт-амперную характеристику контакта в заданном диапазоне температур, дать рекомендации по применению исследуемого контакта.
Таблица 1. Некоторые свойства металлов
No ВАР. |
Элемент | Структура | Атомная масса | Параметр решетки, Å | Плотность, г/см3 | Удельное сопротивление, мкОм·см | Температура, К | Работа выхода φ, эВ | ||
| Дебая (TD) | Ферми (TF·10-4) | плавления (Tпл) | ||||||||
| 14 | Au | ГЦК | 196.9 | 4.08 | 19.28 | 2.2 | 165 | 6.39 | 1337 | 4.58 |
1) Определить класс симметрии заданных материалов, построить прямую и обратную элементарные ячейки заданных материалов. Определить размеры Зоны Бриллюэна в направлениях X, L, К.
Гранецентрированная Кубическая решётка
Формула симметрии: 3L44L36L29PC
Класс симметрии: m3m
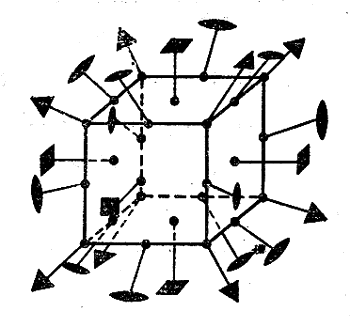
Так как формулы симметрии ГЦК и простой кубической решётки совпадают, приведём на рис. 1-3 изображения осей, плоскостей и центра симметрии для последнего
{width="3.4504in"
height="2.9512in"}
Рис. 1 Изображение осей симметрии кубической решётки
{width="4.5437in"
height="3.0126in"}
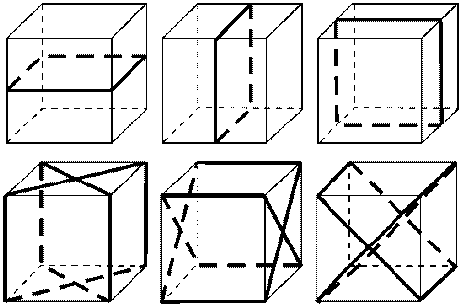
Рис. 2 Изображение плоскостей симметрии куба
{width="2.0882in"
height="2.4307in"}
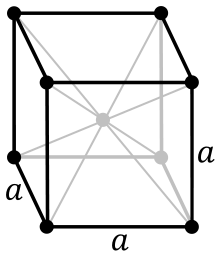
Рис. 3 Изображение центра симметрии куба
Базисные вектора:
$$a_{1} = \begin{bmatrix} \frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}} \ 0 \ \end{bmatrix}$$, $$a_{2} = \begin{bmatrix} \frac{1}{\sqrt{2}} \ 0 \ \frac{1}{\sqrt{2}} \ \end{bmatrix}$$, $$a_{3} = \begin{bmatrix} 0 \ \frac{1}{\sqrt{2}} \ \frac{1}{\sqrt{2}} \ \end{bmatrix}$$, считая, что постоянная решётки = 1
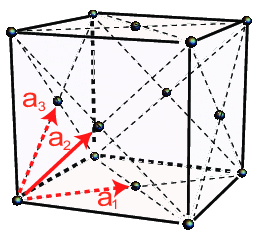
Построим кристаллическую решётку по заданным векторам (рис. 4)
{width="2.6874in"
height="2.4583in"}
Рис. 4 ГЦК
Объём элементарной ячейки:
V = {|{\overrightarrow{a_{1}} \cdot \left\lbrack {\overrightarrow{a_{2}} \times a_{3}} \right\rbrack}|} = \frac{1}{\sqrt{2}}
Базисные вектора обратной решётки:
{a_{i}^{\ast} = \frac{2\pi}{V}}\left\lbrack {a_{j} \times a_{k}} \right\rbrack,{i \neq j \neq k}
$$a_{1}^{\ast} = \begin{bmatrix} {\sqrt{2}\pi} \ {{- \sqrt{2}}\pi} \ {{- \sqrt{2}}\pi} \ \end{bmatrix}$$, $$a_{2}^{\ast} = \begin{bmatrix} {{- \sqrt{2}}\pi} \ {\sqrt{2}\pi} \ {{- \sqrt{2}}\pi} \ \end{bmatrix}$$, $$a_{3}^{\ast} = \begin{bmatrix} {{- \sqrt{2}}\pi} \ {{- \sqrt{2}}\pi} \ {\sqrt{2}\pi} \ \end{bmatrix}$$
Изобразим её на рис. 5
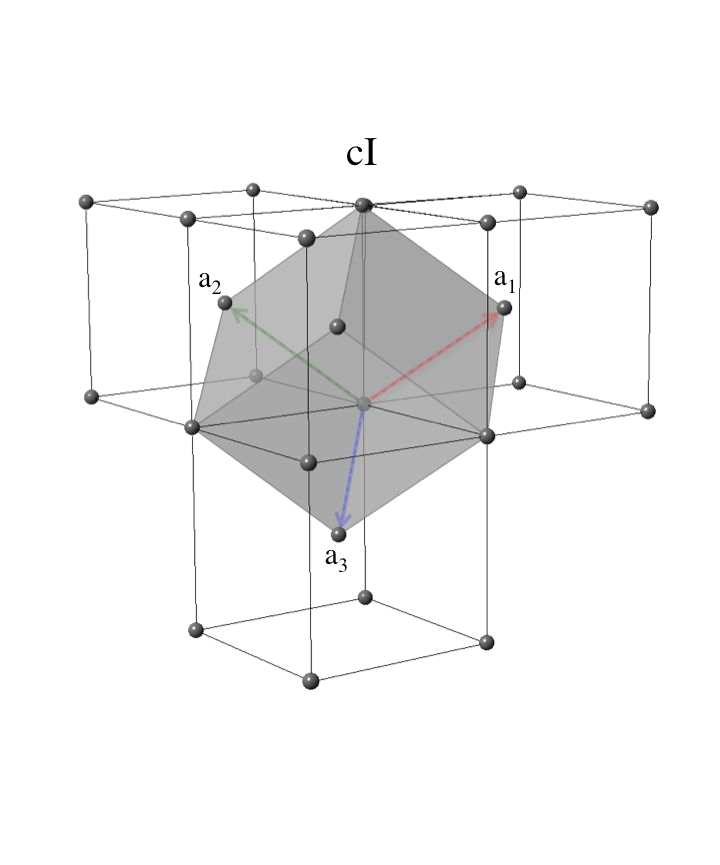{width="4.128in"
height="3.6374in"}
Рис. 5 Обратная решётка ГЦК
Первая зона Бриллюэна (рис. 6):
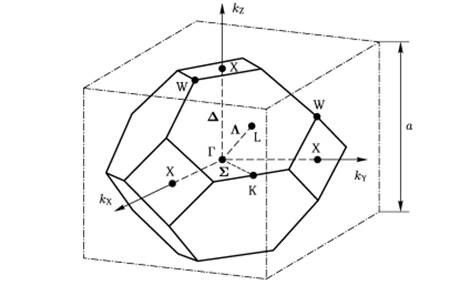{width="4.6874in"
height="2.9689in"}
Рис. 6 Первая зона Бриллюэна
Размеры зоны Бриллюэна по направлениям X, L, K:
$$X = \begin{bmatrix} 0 \ 0 \ 1 \ \end{bmatrix}$$ - центр верхнего квадрата
$$L = \begin{bmatrix} 0.5 \ 0.5 \ 0.5 \ \end{bmatrix}$$ - центр шестиугольника
$$K = \begin{bmatrix} 0.75 \ 0.75 \ 0 \ \end{bmatrix}$$ - середина грани соединяющей два шестиугольника
2) Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов.
В момент касания волновой вектор kф, соответствующий радиусу сферы
Ферми, равен волновому вектору kз, при котором в направлении,
перпендикулярном отражающим плоскостям, выполняется уравнение
Вульфа-Брэггов. Условия касания для двумерной модели можно записать в
виде k_{ф} = k_{з} или, поскольку {k = 2}\frac{\pi}{\lambda}, то
\lambda_{ф} = \lambda_{з}.
Объем сферы Ферми в пространстве импульсов равен
\frac{4}{3}\pi p_{ф}^{3} , где p_{ф} -- импульс электронов на
поверхности Ферми. С другой стороны, этот же объем равен
\frac{N}{2}\frac{h^{3}}{V}, где N -- число электронов в объеме V.
Таким образом:
\frac{4}{3}\pi{p_{ф}^{3} = \frac{N}{2}}\frac{h^{3}}{V}
Откуда находим:
{p_{ф} = h}\left( \frac{3N}{8\pi V} \right)^{1/3}
Поскольку по соотношению де-Бройля \lambda = \frac{h}{p}, то
\lambda_{ф} = \left( \frac{8\pi V}{3N} \right)^{1/3}
Найдем теперь λз. Из всех граней первой зоны Бриллюэна для
гранецентрированной решетки ближе всего к началу координат находятся
грани, обусловленные отражением электронов от плоскостей {111}. Поэтому
сфера Ферми впервые коснется именно этих граней. Таким образом, для
определения условий касания сферы с первой зоной Бриллюэна необходимо
найти длину волны, при которой электроны взаимодействуют с плоскостями
{111}. Из уравнения Вульфа -- Бреггов
{\mathit{n\lambda} = 2}d\mathit{sin\theta} находим:
3
{\lambda_{з} = 2}{d = 2}{\frac{a}{\sqrt{H^{2} + K^{2} + L^{2}}} = 2}\frac{a}{\sqrt{3}}
(здесь θ = 90°, так как в точке касания волновой вектор перпендикулярен к плоскостям {111}; п = 1, так как λ--наибольшее)
Если в объеме V число атомов Na, то число элементарных ячеек будет
\frac{N_{a}}{4}, так как на одну ячейку гранецентрированной решетки
приходится четыре атома, тогда {V = a^{3}}\frac{N_{a}}{4}
Откуда a = \left( \frac{4V}{N_{a}} \right)^{1/3}, следовательно
{\lambda_{з} = \frac{2}{\sqrt{3}}}\left( \frac{4V}{N_{a}} \right)^{1/3}
Возводя обе части этого тождества в куб и произведя необходимые сокращения, получаем:
\frac{N}{N_{a}} = \frac{\pi\sqrt{3}}{4} = 1.36
Список литературы:
Астанин В.В. Физика твёрдого тела