radiostatistics/1.md

papersize	fontsize	geometry	header-includes
a4	14pt	margin=20mm	\usepackage{fontspec} \usepackage{unicode-math} \setmainfont{DejaVu Serif}

I. Построение алгоритма обнаружителя

w(x_1, \dots, x_n | H_0) = \begin{cases}
    \prod_{i=1}^{n} \frac{1}{\mu} e^{-\frac{x_i}{\mu}}, & x_i \ge 0, \quad i = \overline{1 \dots n} \\
    0, & \exists i: x_i < 0
\end{cases}

w(x_1, \dots, x_n | H_1) = \begin{cases}
    \prod_{i=1}^{n} \frac{1}{\mu} e^{-\frac{x_i-u}{\mu}}, & x_i \ge u, \quad i = \overline{1 \dots n} \\
    0, & \exists i: x_i < u
\end{cases}

L = \dfrac{w(x_1, \dots, x_n | H_1)}{w(x_1, \dots, x_n | H_0)} \gtrless^{H_1^*}_{H_0^*} L_{\text{пор}}

L = \begin{cases}
    \dfrac{0}{0}, & \exists i: x_i < 0 \\
    \dfrac{0}{\prod_{i=1}^{n} \frac{1}{\mu} e^{-\frac{x_i}{\mu}}}, & (x_i \ge 0, \quad i = \overline{1 \dots n}) \cap (\exists i: x_i < u) \\
    \dfrac{\prod_{i=1}^{n} \frac{1}{\mu} e^{-\frac{x_i-u}{\mu})}}{\prod_{i=1}^{n} \frac{1}{\mu} e^{-\frac{x_i}{\mu}}}, & x_i \ge u, \quad i = \overline{1 \dots n}
\end{cases}

\tag{1}
L = \begin{cases}
    \textrm{undefined}, & \exists i: x_i < 0 \\
    0, & (x_i \ge 0, \quad i = \overline{1 \dots n}) \cap (\exists i: x_i < u) \\
    e^{n \frac{u}{\mu}}, & x_i \ge u, \quad i = \overline{1 \dots n}
\end{cases}

II. Нахождение теоретических кривых обнаружения

Вероятность ложной тревоги:

\alpha = P(H_1^* | H_0) = P(L > L_{\text{пор}} | H_0)

1. L_{\text{пор}} \in [0, e^{n \frac{u}{\mu}})

\alpha = P(x_i \ge u, \quad i = \overline{1 \dots n} | H_0) = \prod_{i=1}^n P(x_i \ge u | H_0) P(x_i \ge u | H_0) = 1 - P(x_i < u | H_0) = 1 - F_{\exp}(u) = 1 - (1 - e^{-\frac{u}{\mu}}) = e^{- \frac{u}{\mu}}

\tag{2}
\alpha = \prod_{i=1}^n e^{-\frac{u}{\mu}} = e^{-n \frac{u}{\mu}}

2. L_{\text{пор}} < 0

\alpha = P((x_i \ge 0, \quad i = \overline{1 \dots n}) \cap (\exists i: x_i < u) | H_0) + P(x_i \ge u, \quad i = \overline{1 \dots n} | H_0) P((x_i \ge 0, \quad i = \overline{1 \dots n}) \cap (\exists i: x_i < u) | H_0) = \prod_{i=1}^n P(x_i \ge 0 | H_0) \cdot \left[ 1 - \prod_{i=1}^n P(x_i \ge u | H_0) \right] P(x_i \ge 0 | H_0) = 1 - F_{\exp}(0) = 1 \alpha = 1

\pagebreak

3. L_{\text{пор}} \ge e^{n \frac{u}{\mu}}

\alpha = 0

Вероятность правильного обнаружения

D = P(H_1^* | H_1) = P(L > L_{\text{пор}} | H_1)

1. L_{\text{пор}} \in [0, e^{n \frac{u}{\mu}})

D = P(x_i \ge u, \quad i = \overline{1 \dots n} | H_1) = \prod_{i=1}^n P(x_i \ge u | H_1) P(x_i \ge u|H_1) = 1 - P(x_i < u | H_1) = 1 - F_{\exp}(0) = 1 D = 1

2. L_{\text{пор}} < 0

D = P((x_i \ge 0, \quad i = \overline{1 \dots n}) \cap (\exists i: x_i < u) | H_1) + P(x_i \ge u, \quad i = \overline{1 \dots n} | H_1) P((x_i \ge 0, \quad i = \overline{1 \dots n}) \cap (\exists i: x_i < u) | H_1) = \prod_{i=1}^n P(x_i \ge 0 | H_1) \cdot \left[ 1 - \prod_{i=1}^n P(x_i \ge u | H_1) \right] P(x_i \ge 0 | H_1) = 1 D = 1 \cdot (1 - 1) + 1 = 1

3. L_{\text{пор}} \ge e^{n \frac{u}{\mu}}

D = 0

Зависимость вероятности правильного обнаружения от вероятности ложной тревоги:

\tag{3}
D = \begin{cases}
    1, & \alpha > 0 \\
    0, & \alpha = 0
\end{cases}

III. Экспериментальные кривые обнаружения

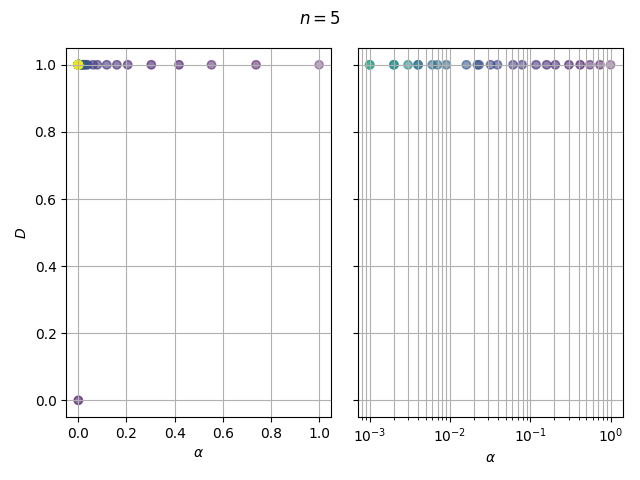
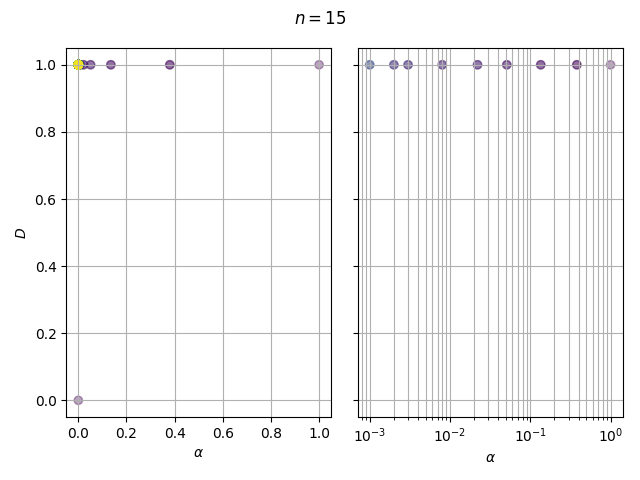
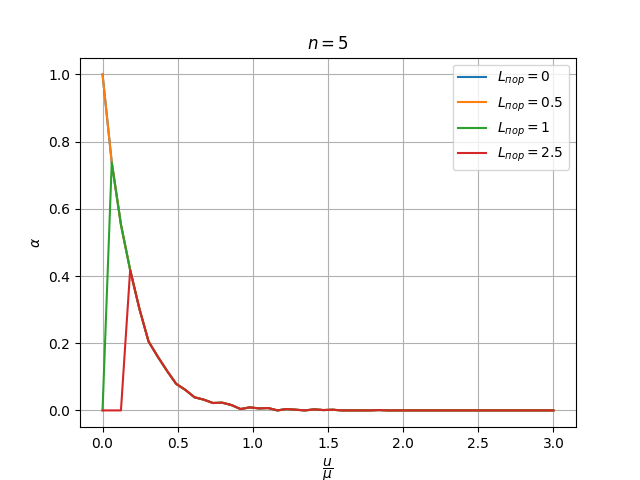
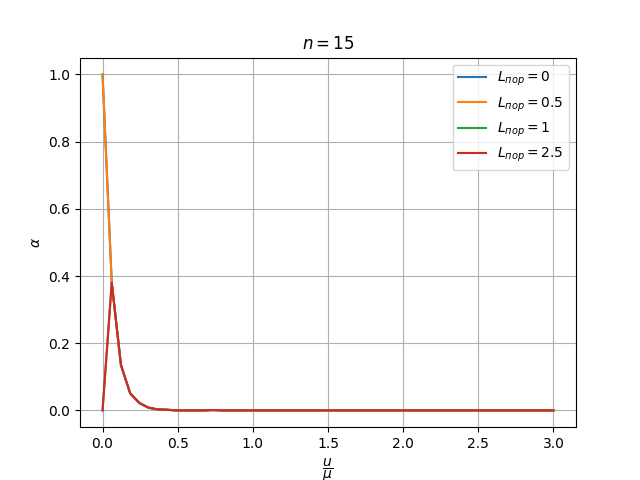
В нотбуке 1.ipynb выполняется моделирование полученного алгоритма обнаружения. Результаты также приводятся ниже:

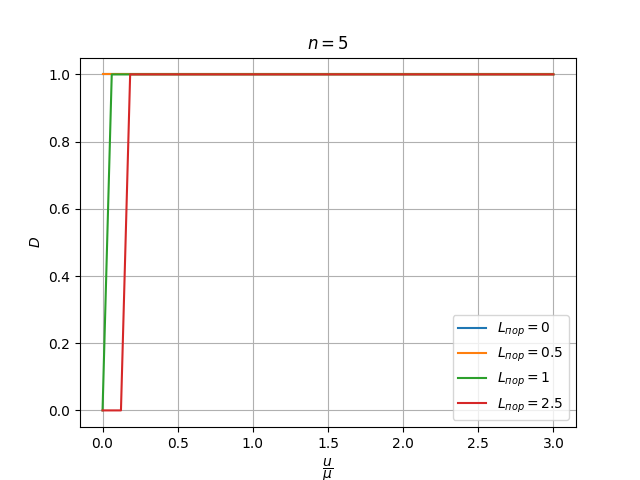
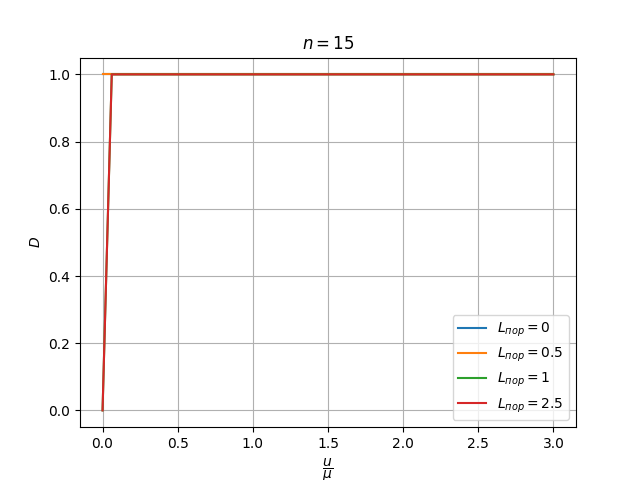
Кривые обнаружения соответствуют теории (3). Распределение экспериментальных значений вероятности ложной тревоги при линейном изменении отношения \frac{u}{\mu} соответствует закону их взаимозависимости (2).

Зависимость вероятности правильного обнаружения от отношения уровня сигнала к масштабному коэффициенту распределения шума равна 1 всюду кромее "отсечки" в 0 при низких соотношениях сигнал/шум, когда L_{\text{пор}} оказывается выше e^{n \frac{u}{\mu}}

Вероятность ложной тревоги также отсекается в 0 при больших L_{\text{пор}}.