Polynomial Interpolation

ANSI C program which composes polynomial of n - 1 degree that passes through n dots. It presents it in Newton interpolation polynomial and monic form.

Interface

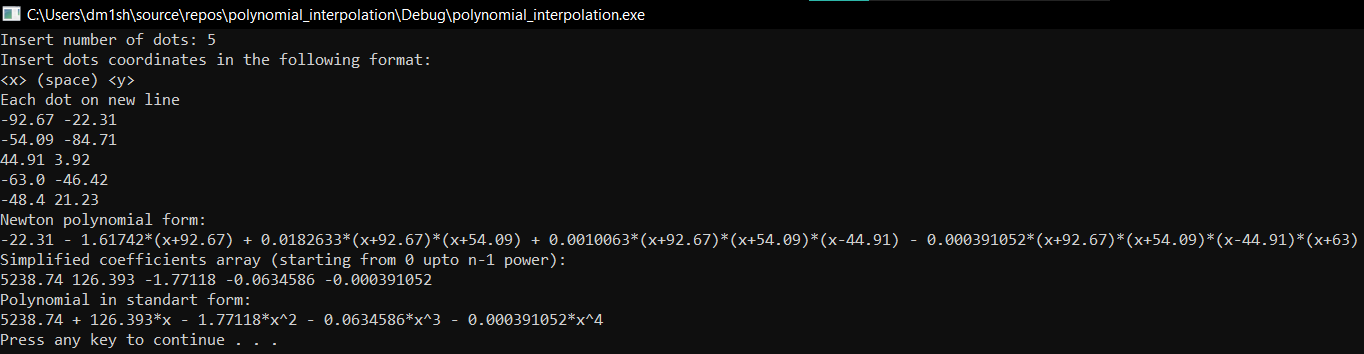
Application accepts as standart input decimal below 2147483647 n as number of dots, followed by n dots in format: <x> (space) <y> on each line, where x is an abscisse and y is an ordinate of single dot. Dot coordinates must fit [2.22507e-308;1.79769e+308] range by modulo.

Result will be printed to standart output in the following format:

Newton polynomial form:

f_0 - f_1*(x-x_0) + ... + f_n(x-x_0)*(x-x_1)*...*(x-x_{n-1})

Simplified coefficients array (starting from 0 upto n-1 power):

a_0 a_1 ... a_{n-1} a_n

Polynomial in monic form:

a_0 - a_1*x + ... + a_{n-1}*x^(n-2) + a_n*x^(n-1)

Where f_i is a divided difference of y_1,...,y_i, a_i are coefficients of resulting monic polynomial

Data structure

• n is an unsigned int variable, that is used to input and store number of dots

• x is a pointer to array of n doubles, that is used to store abscisses of dots

• y is a pointer to array of n doubles, that is used to store ordinates of dots

• coefficients is a pointer to array of n doubles, that is used to store coefficients of monic interpolation polynomial

• i, j are int variables, those are used in loops as iterators

• tmp_polynomial is a pointer to array of n doubles, that is used to store coefficients of polynomial, resulting during simplification of interpolation polynomial summands.

Example

Build and run application:

gcc main.c
./a.out

Input/output

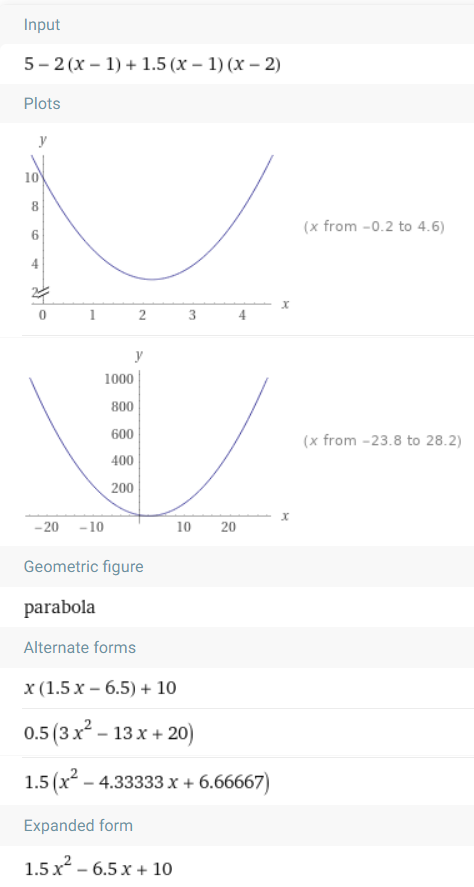
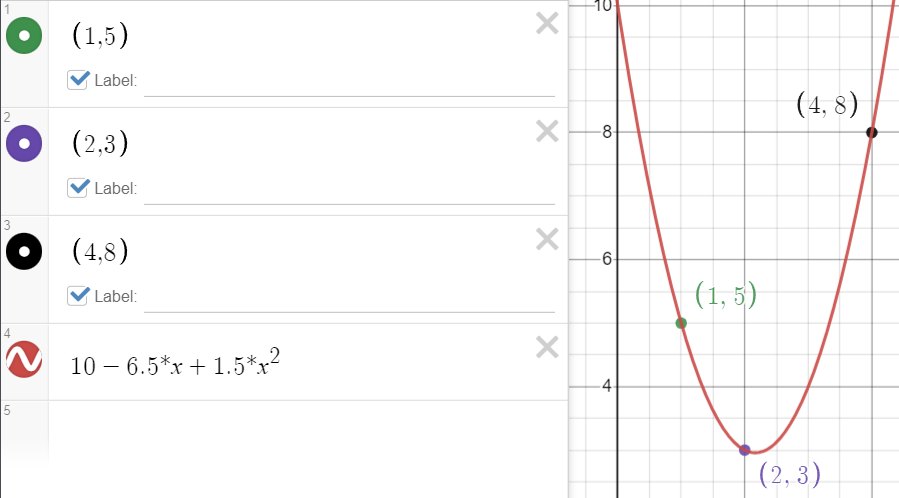
For input n = 3 and the following dots

1 5
2 3
4 8

Output is

Newton polynomial form:
5 - 2*(x-1) + 1.5*(x-1)*(x-2)
Simplified coefficients array (starting from 0 upto n-1 power):
10 -6.5 1.5
Polynomial in standart form:
10 - 6.5*x + 1.5*x^2

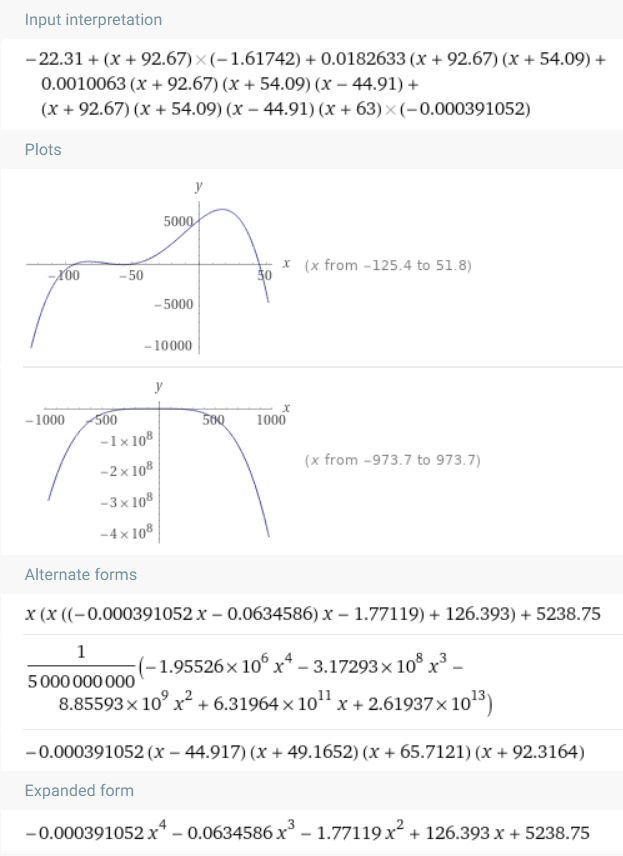
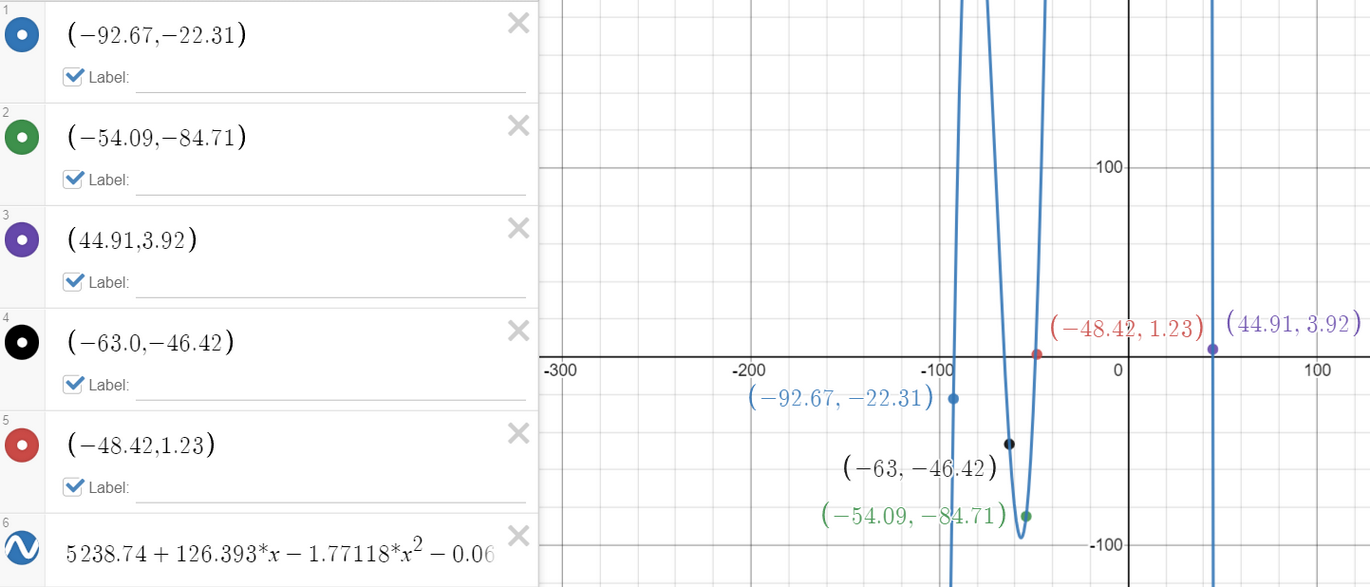
Illustrations

Example 1

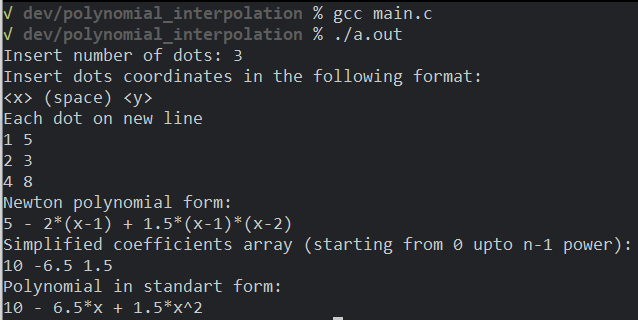
Example 2

or