48 KiB
Практическая работа №2
Вариант 6
Таблица находится в конце файла. Так же все файлы проекта (в том числе отчёт в формате odt или pdf) можно скачать с git: https://git.dm1sh.ru/data-visualization/practice2
Изначально проект писался в vscode под линуксом, если не работает установка пакетов в первом блоке, попробуйте заменить % на ! или установить пакеты вручную и удалить его
- Подгружаем нужные для работы пакеты
# установка matplotlib, numpy и pandas
%pip install matplotlib numpy pandas seaborn --upgrade
Requirement already satisfied: matplotlib in ./.venv/lib64/python3.11/site-packages (3.7.1)
Requirement already satisfied: numpy in ./.venv/lib64/python3.11/site-packages (1.24.2)
Requirement already satisfied: pandas in ./.venv/lib64/python3.11/site-packages (1.5.3)
Requirement already satisfied: seaborn in ./.venv/lib64/python3.11/site-packages (0.12.2)
Requirement already satisfied: contourpy>=1.0.1 in ./.venv/lib64/python3.11/site-packages (from matplotlib) (1.0.7)
Requirement already satisfied: cycler>=0.10 in ./.venv/lib64/python3.11/site-packages (from matplotlib) (0.11.0)
Requirement already satisfied: fonttools>=4.22.0 in ./.venv/lib64/python3.11/site-packages (from matplotlib) (4.38.0)
Requirement already satisfied: kiwisolver>=1.0.1 in ./.venv/lib64/python3.11/site-packages (from matplotlib) (1.4.4)
Requirement already satisfied: packaging>=20.0 in ./.venv/lib64/python3.11/site-packages (from matplotlib) (23.0)
Requirement already satisfied: pillow>=6.2.0 in ./.venv/lib64/python3.11/site-packages (from matplotlib) (9.4.0)
Requirement already satisfied: pyparsing>=2.3.1 in ./.venv/lib64/python3.11/site-packages (from matplotlib) (3.0.9)
Requirement already satisfied: python-dateutil>=2.7 in ./.venv/lib64/python3.11/site-packages (from matplotlib) (2.8.2)
Requirement already satisfied: pytz>=2020.1 in ./.venv/lib64/python3.11/site-packages (from pandas) (2022.7.1)
Requirement already satisfied: six>=1.5 in ./.venv/lib64/python3.11/site-packages (from python-dateutil>=2.7->matplotlib) (1.16.0)
[notice] A new release of pip available: 22.2.2 -> 23.0.1
[notice] To update, run: pip install --upgrade pip
Note: you may need to restart the kernel to use updated packages.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
- Загружаем данные. Они представляют результаты эксперимента по выявлению дефектов в подшипниковых узлах жидкостного трения. Время эксперимента 10 мин. Частота получения данных о колебаниях ротора 1000 сиг/сек. Частота съема данных о температуре 1 сиг/сек. В работе используются набор данных с и без дефектов. Задача: выявить выбросы в данных, найти переходный период, в течение которого система выходит на режим, выяснить, в каких атрибутах наиболее ярко выражаются отличия в экспериментах с дефектами и без, а так же можно ли на этапе переходного периода говорить о наличии дефекта.
- Набор данных без дефектов
df_norm = pd.read_csv('./data_5_1.csv')
display(df_norm.info())
display(df_norm.describe())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 601000 entries, 0 to 600999
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Fluctuations_X_in_the_left_bearing 601000 non-null float64
1 Fluctuations_Y_in_the_left_bearing 601000 non-null float64
2 Fluctuations_X_in_the_right_bearing 601000 non-null float64
3 Fluctuations_Y_in_the_right_bearing 601000 non-null float64
4 Fluctuations_X_in_the_left_bearing_smooth 601000 non-null float64
5 Fluctuations_Y_in_the_left_bearing_smooth 601000 non-null float64
6 Fluctuations_X_in_the_right_bearing_smooth 601000 non-null float64
7 Fluctuations_Y_in_the_right_bearing_smooth 601000 non-null float64
8 Temperature_in_the_left_bearing 601000 non-null float64
9 Temperature_in_the_right_bearing 601000 non-null float64
dtypes: float64(10)
memory usage: 45.9 MB
None
| Fluctuations_X_in_the_left_bearing | Fluctuations_Y_in_the_left_bearing | Fluctuations_X_in_the_right_bearing | Fluctuations_Y_in_the_right_bearing | Fluctuations_X_in_the_left_bearing_smooth | Fluctuations_Y_in_the_left_bearing_smooth | Fluctuations_X_in_the_right_bearing_smooth | Fluctuations_Y_in_the_right_bearing_smooth | Temperature_in_the_left_bearing | Temperature_in_the_right_bearing |
|---|---|---|---|---|---|---|---|---|---|
| count | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 |
| mean | 5.455242 | 6.335448 | 5.691674 | 7.220008 | 5.455247 | 6.335445 | 5.691669 | 7.220007 | 1108.853443 |
| std | 0.084957 | 0.100096 | 0.079720 | 0.077585 | 0.071788 | 0.081333 | 0.065328 | 0.063549 | 4.983924 |
| min | 5.032000 | 5.818000 | 5.152000 | 6.745000 | 5.201000 | 6.022000 | 5.442000 | 6.993000 | 1091.353000 |
| 25% | 5.388000 | 6.263000 | 5.635000 | 7.164000 | 5.390000 | 6.264000 | 5.636000 | 7.165000 | 1106.737000 |
| 50% | 5.463000 | 6.332000 | 5.692000 | 7.212000 | 5.465000 | 6.331000 | 5.691000 | 7.211000 | 1110.546000 |
| 75% | 5.521000 | 6.410000 | 5.749000 | 7.276000 | 5.520000 | 6.407000 | 5.744000 | 7.274000 | 1112.673000 |
| max | 6.089000 | 7.171000 | 6.362000 | 8.006000 | 5.744000 | 6.734000 | 6.001000 | 7.578000 | 1113.476000 |
- Набор данных с наличием несоосности в муфте
df_misal = pd.read_csv('./data_4_2.csv')
display(df_misal.info())
display(df_misal.describe())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 601000 entries, 0 to 600999
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Fluctuations_X_in_the_left_bearing 601000 non-null float64
1 Fluctuations_Y_in_the_left_bearing 601000 non-null float64
2 Fluctuations_X_in_the_right_bearing 601000 non-null float64
3 Fluctuations_Y_in_the_right_bearing 601000 non-null float64
4 Fluctuations_X_in_the_left_bearing_smooth 601000 non-null float64
5 Fluctuations_Y_in_the_left_bearing_smooth 601000 non-null float64
6 Fluctuations_X_in_the_right_bearing_smooth 601000 non-null float64
7 Fluctuations_Y_in_the_right_bearing_smooth 601000 non-null float64
8 Temperature_in_the_left_bearing 601000 non-null float64
9 Temperature_in_the_right_bearing 601000 non-null float64
dtypes: float64(10)
memory usage: 45.9 MB
None
| Fluctuations_X_in_the_left_bearing | Fluctuations_Y_in_the_left_bearing | Fluctuations_X_in_the_right_bearing | Fluctuations_Y_in_the_right_bearing | Fluctuations_X_in_the_left_bearing_smooth | Fluctuations_Y_in_the_left_bearing_smooth | Fluctuations_X_in_the_right_bearing_smooth | Fluctuations_Y_in_the_right_bearing_smooth | Temperature_in_the_left_bearing | Temperature_in_the_right_bearing |
|---|---|---|---|---|---|---|---|---|---|
| count | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 |
| mean | 4.984535 | 6.652319 | 5.795459 | 7.310637 | 4.984530 | 6.652318 | 5.795455 | 7.310634 | 1107.421877 |
| std | 0.069982 | 0.108803 | 0.088409 | 0.088030 | 0.052889 | 0.092470 | 0.075171 | 0.075327 | 3.960030 |
| min | 4.526000 | 6.121000 | 5.345000 | 6.751000 | 4.773000 | 6.324000 | 5.541000 | 6.959000 | 1100.641000 |
| 25% | 4.935000 | 6.572000 | 5.733000 | 7.257000 | 4.942000 | 6.573000 | 5.734000 | 7.261000 | 1103.898000 |
| 50% | 4.995000 | 6.636000 | 5.795000 | 7.303000 | 4.995000 | 6.636000 | 5.792000 | 7.302000 | 1107.961000 |
| 75% | 5.027000 | 6.738000 | 5.860000 | 7.371000 | 5.021000 | 6.735000 | 5.856000 | 7.370000 | 1110.810000 |
| max | 5.635000 | 7.505000 | 6.544000 | 8.087000 | 5.298000 | 7.047000 | 6.114000 | 7.654000 | 1113.633000 |
- Набор данных с наличием дисбаланса
df_disbal = pd.read_csv('./data_4_3.csv')
display(df_disbal.info())
display(df_disbal.describe())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 601000 entries, 0 to 600999
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Fluctuations_X_in_the_left_bearing 601000 non-null float64
1 Fluctuations_Y_in_the_left_bearing 601000 non-null float64
2 Fluctuations_X_in_the_right_bearing 601000 non-null float64
3 Fluctuations_Y_in_the_right_bearing 601000 non-null float64
4 Fluctuations_X_in_the_left_bearing_smooth 601000 non-null float64
5 Fluctuations_Y_in_the_left_bearing_smooth 601000 non-null float64
6 Fluctuations_X_in_the_right_bearing_smooth 601000 non-null float64
7 Fluctuations_Y_in_the_right_bearing_smooth 601000 non-null float64
8 Temperature_in_the_left_bearing 601000 non-null float64
9 Temperature_in_the_right_bearing 601000 non-null float64
dtypes: float64(10)
memory usage: 45.9 MB
None
| Fluctuations_X_in_the_left_bearing | Fluctuations_Y_in_the_left_bearing | Fluctuations_X_in_the_right_bearing | Fluctuations_Y_in_the_right_bearing | Fluctuations_X_in_the_left_bearing_smooth | Fluctuations_Y_in_the_left_bearing_smooth | Fluctuations_X_in_the_right_bearing_smooth | Fluctuations_Y_in_the_right_bearing_smooth | Temperature_in_the_left_bearing | Temperature_in_the_right_bearing |
|---|---|---|---|---|---|---|---|---|---|
| count | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 |
| mean | 5.459564 | 6.337034 | 5.668791 | 7.144426 | 5.459570 | 6.337033 | 5.668790 | 7.144428 | 1109.347354 |
| std | 0.094292 | 0.104977 | 0.081341 | 0.079577 | 0.082518 | 0.087532 | 0.067253 | 0.065966 | 3.584635 |
| min | 4.979000 | 5.824000 | 5.212000 | 6.661000 | 5.187000 | 6.022000 | 5.414000 | 6.892000 | 1097.972000 |
| 25% | 5.382000 | 6.256000 | 5.608000 | 7.086000 | 5.383000 | 6.258000 | 5.611000 | 7.089000 | 1108.479000 |
| 50% | 5.458000 | 6.336000 | 5.674000 | 7.151000 | 5.459000 | 6.336000 | 5.675000 | 7.151000 | 1110.300000 |
| 75% | 5.539000 | 6.419000 | 5.729000 | 7.200000 | 5.537000 | 6.416000 | 5.725000 | 7.198000 | 1111.793000 |
| max | 6.118000 | 7.173000 | 6.346000 | 7.888000 | 5.756000 | 6.742000 | 5.985000 | 7.448000 | 1113.015000 |
- Набор данных со втулкой с дефектами
df_defect = pd.read_csv('./data_4_4.csv')
display(df_defect.info())
display(df_defect.describe())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 601000 entries, 0 to 600999
Data columns (total 10 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Fluctuations_X_in_the_left_bearing 601000 non-null float64
1 Fluctuations_Y_in_the_left_bearing 601000 non-null float64
2 Fluctuations_X_in_the_right_bearing 601000 non-null float64
3 Fluctuations_Y_in_the_right_bearing 601000 non-null float64
4 Fluctuations_X_in_the_left_bearing_smooth 601000 non-null float64
5 Fluctuations_Y_in_the_left_bearing_smooth 601000 non-null float64
6 Fluctuations_X_in_the_right_bearing_smooth 601000 non-null float64
7 Fluctuations_Y_in_the_right_bearing_smooth 601000 non-null float64
8 Temperature_in_the_left_bearing 601000 non-null float64
9 Temperature_in_the_right_bearing 601000 non-null float64
dtypes: float64(10)
memory usage: 45.9 MB
None
| Fluctuations_X_in_the_left_bearing | Fluctuations_Y_in_the_left_bearing | Fluctuations_X_in_the_right_bearing | Fluctuations_Y_in_the_right_bearing | Fluctuations_X_in_the_left_bearing_smooth | Fluctuations_Y_in_the_left_bearing_smooth | Fluctuations_X_in_the_right_bearing_smooth | Fluctuations_Y_in_the_right_bearing_smooth | Temperature_in_the_left_bearing | Temperature_in_the_right_bearing |
|---|---|---|---|---|---|---|---|---|---|
| count | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 | 601000.000000 |
| mean | 5.343087 | 6.470311 | 6.011416 | 7.066158 | 5.343089 | 6.470312 | 6.011420 | 7.066161 | 1109.685379 |
| std | 0.092243 | 0.082721 | 0.071645 | 0.072093 | 0.079303 | 0.058977 | 0.056743 | 0.054376 | 5.512947 |
| min | 4.882000 | 5.900000 | 5.614000 | 6.548000 | 5.044000 | 6.205000 | 5.792000 | 6.859000 | 1092.609000 |
| 25% | 5.266000 | 6.417000 | 5.964000 | 7.021000 | 5.268000 | 6.419000 | 5.967000 | 7.024000 | 1106.780000 |
| 50% | 5.346000 | 6.476000 | 6.003000 | 7.060000 | 5.348000 | 6.476000 | 6.001000 | 7.059000 | 1111.812000 |
| 75% | 5.419000 | 6.522000 | 6.062000 | 7.110000 | 5.417000 | 6.519000 | 6.056000 | 7.107000 | 1114.155000 |
| max | 6.073000 | 7.247000 | 6.747000 | 7.795000 | 5.656000 | 6.814000 | 6.300000 | 7.413000 | 1115.813000 |
- На основании приведённого выше описания, можно сказать, что pandas верно справился с определением типа - все 10 параметров имеют вещественный (float64) тип данных. Что соответствует исходным данным:
-
1 столбец массива -
Fluctuations_X_in_the_left_bearing- горизонтальные колебания в левом подшипнике, в Вольтах -
2 столбец массива -
Fluctuations_Y_in_the_left_bearing- вертикальные колебания в левом подшипнике, в Вольтах -
3 столбец массива -
Fluctuations_X_in_the_right_bearing- горизонтальные колебания в правом подшипнике, в Вольтах -
4 столбец массива -
Fluctuations_Y_in_the_right_bearing- вертикальные колебания в правом подшипнике подшипнике, в Вольтах -
5 столбец массива -
Fluctuations_X_in_the_left_bearing_smooth- горизонтальные колебания в левом подшипнике с учетом сглаживания, в Вольтах -
6 столбец массива -
Fluctuations_Y_in_the_left_bearing_smooth- вертикальные колебания в левом подшипнике с учетом сглаживания, в Вольтах -
7 столбец массива -
Fluctuations_X_in_the_right_bearing_smooth- горизонтальные колебания в правом подшипнике с учетом сглаживания, в Вольтах -
8 столбец массива -
Fluctuations_Y_in_the_right_bearing_smooth- вертикальные колебания в правом подшипнике подшипнике с учетом сглаживания, в Вольтах -
9 столбец массива -
Temperature_in_the_left_bearing- температура в левом подшипнике, в Омах -
10 столбец массива -
Temperature_in_the_right_bearing- температура в правом подшипнике, в Омах
# Для удобства итерации создадим кортежи с датафреймами, их читабельными именами для подписей и цветами
dfs = (df_norm, df_misal, df_disbal, df_defect)
df_names = ("Без дефектов", "Несоосность в трубке", "Дисбаланс", "Втулка с дефектом")
df_colors = ("tab:blue", "tab:orange", "tab:red", "tab:purple")
# Шкала времени для 1000 зап/сек
time = np.arange(0, df_norm.shape[0]/1000, 0.001)
import itertools as itt
pic_n_gen = itt.count(1) # Счётчик для номеров рисунков
Линейные графики
- Построим линейные графики для флуктуаций и температур для каждого из наборов данных
a4figsize = (8, 11) # размер листа А4 в дюймах
def plot_linear(df, fields, suptitle, xcoord, ylabel, ylim, figsize = a4figsize, linewidth=0.5, color=None):
fig, ax = plt.subplots(len(fields), figsize=figsize, sharex=True, sharey=True)
fig.suptitle(suptitle)
fig.supxlabel(f"Рисунок {next(pic_n_gen)}")
for j, field in enumerate(fields):
ax[j].plot(xcoord, df[field], linewidth=linewidth, color=color)
ax[j].set_ylabel(ylabel)
ax[j].set_title(field)
ax[j].spines['top'].set_visible(False)
ax[j].spines['right'].set_visible(False)
ax[j].set_xlim((np.min(xcoord), np.max(xcoord)))
ax[j].set_ylim(ylim)
ax[-1].set_xlabel("Время, с")
fig.tight_layout()
for i, df in enumerate(dfs):
plot_linear(
df,
fields=df.keys()[:-2],
suptitle=df_names[i],
xcoord=time,
ylabel="Вольты",
ylim=(np.min(df.min()[:-2]), np.max(df.max()[:-2])), # растягиваем график на всю высоту флуктуаций при одинаковых границах для всех
color=df_colors[i]
)
plot_linear(
df,
fields=df.keys()[-2:],
suptitle=df_names[i],
xcoord=time,
ylabel="Омы",
ylim=(np.min(df.min()[-2:]), np.max(df.max()[-2:])), # растягиваем график на всю высоту температур при одинаковых границах для всех
figsize=(8,5),
linewidth=1,
color=df_colors[i]
)
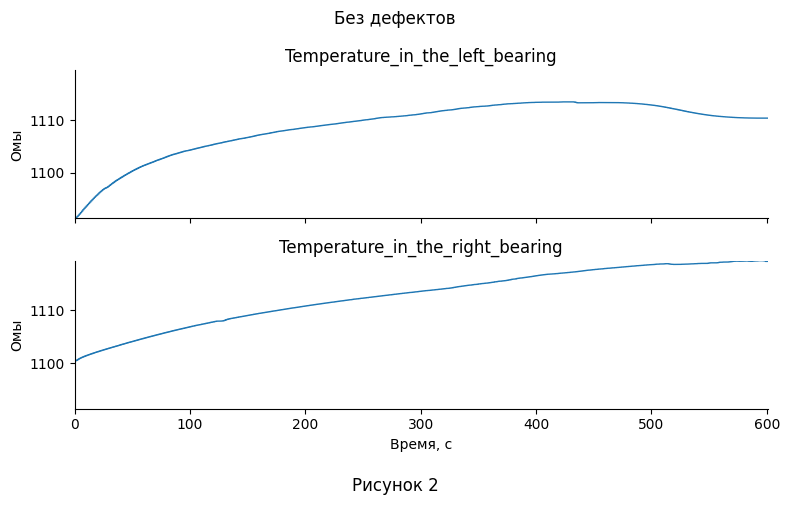
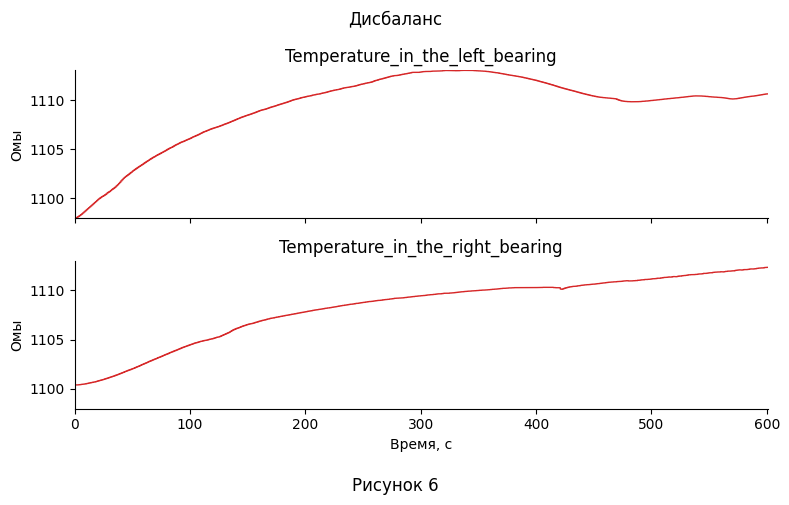
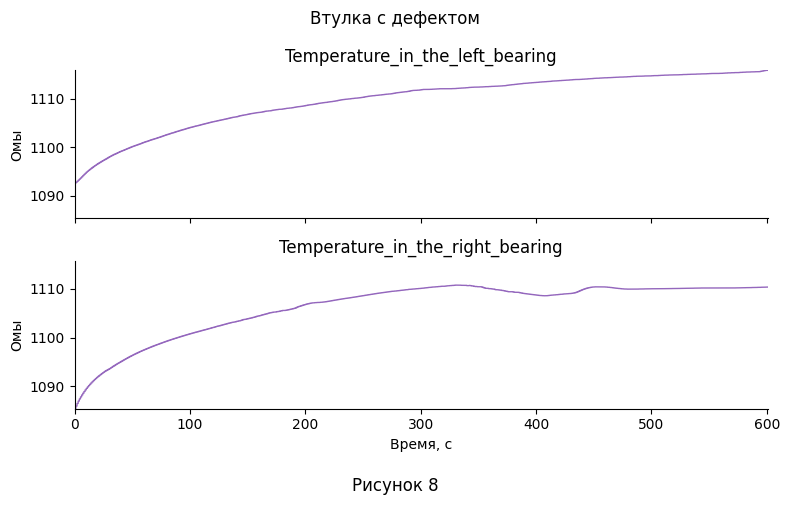
- Из построенных графиков видно, что линейное представление флуктуаций несёт мало информации, поэтому в дальнейшем будут исследоваться только распределение и корреляция между этими признаками. С другой стороны, график температуры имеет ясно различимую временную зависимость, поэтому для него имеет смысл рассмотреть её, а так же корреляцию.
Распределение флуктуаций
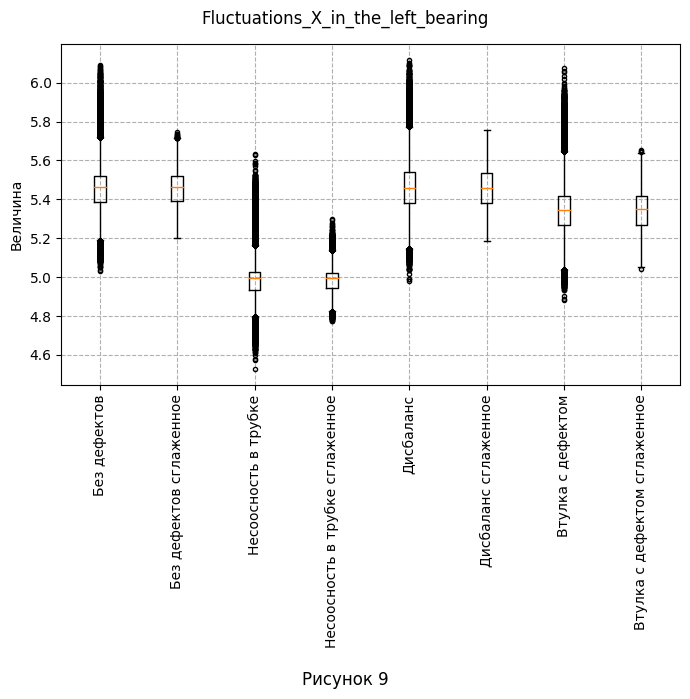
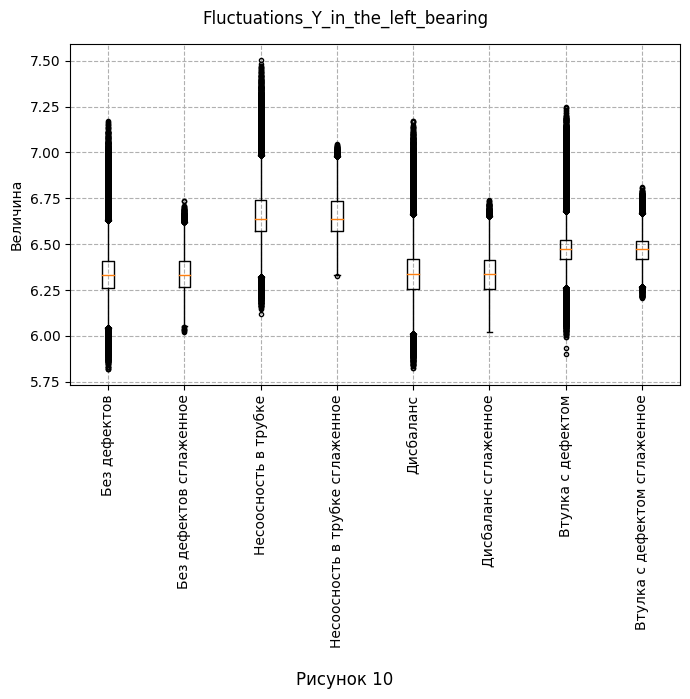
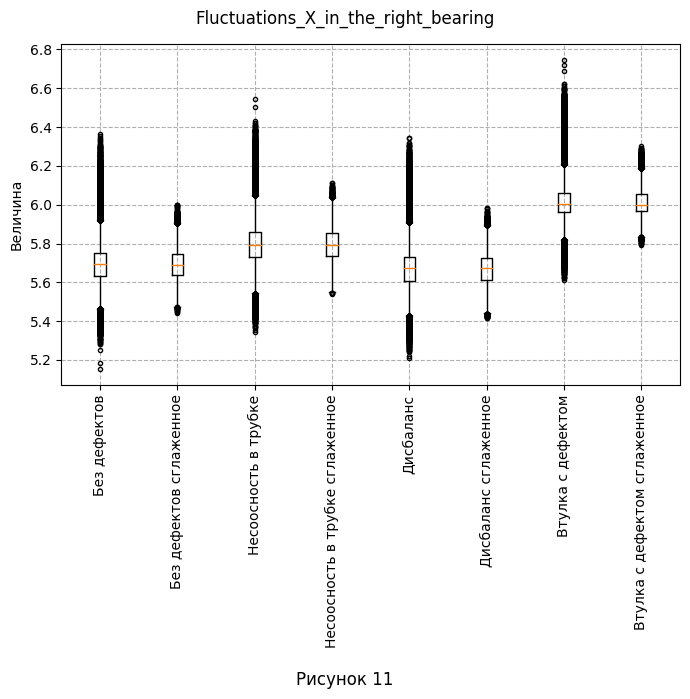
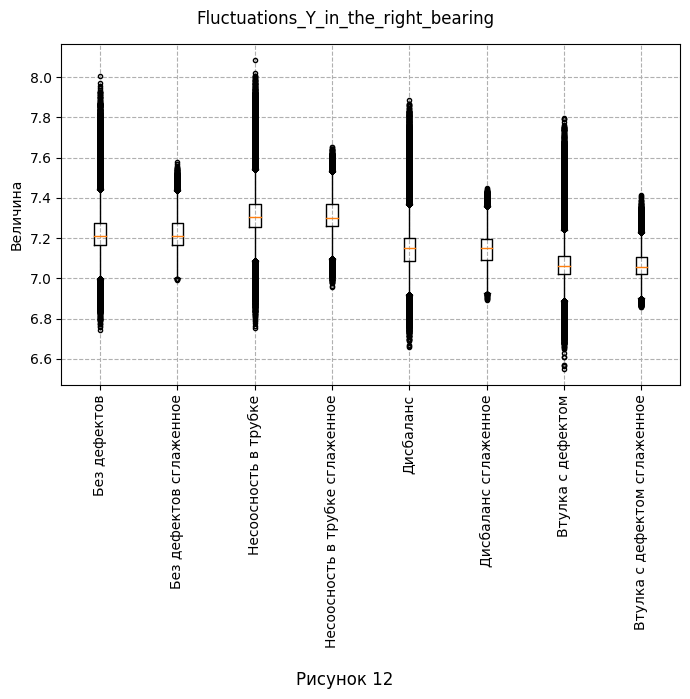
- Как отмечалось в предыдущем пункте, проанализируем распределение для полей, отражающих флуктуации. Первым делом визуализируем данные с помощью так называемого "Ящика с усами". На каждом графике отобразим одну из четырёх флуктуаций и сглаженную версию для каждого набора данных.
for i in range(4):
fig, ax = plt.subplots(figsize=(7, 7))
plt.xticks(rotation=90)
fig.suptitle(df_norm.keys()[i])
fig.supxlabel(f"Рисунок {next(pic_n_gen)}")
flierprops = dict(marker='o', markersize=3)
for j, df in enumerate(dfs):
ax.boxplot(df[df.keys()[i]], positions=[j*2], flierprops=flierprops)
ax.boxplot(df[df.keys()[i+4]], positions=[j*2+1], flierprops=flierprops)
ax.set_ylabel("Величина")
ax.set_xticks(range(8), itt.chain.from_iterable((df_names[j], df_names[j]+" сглаженное") for j in range(4)))
ax.grid(linestyle='--')
fig.tight_layout()
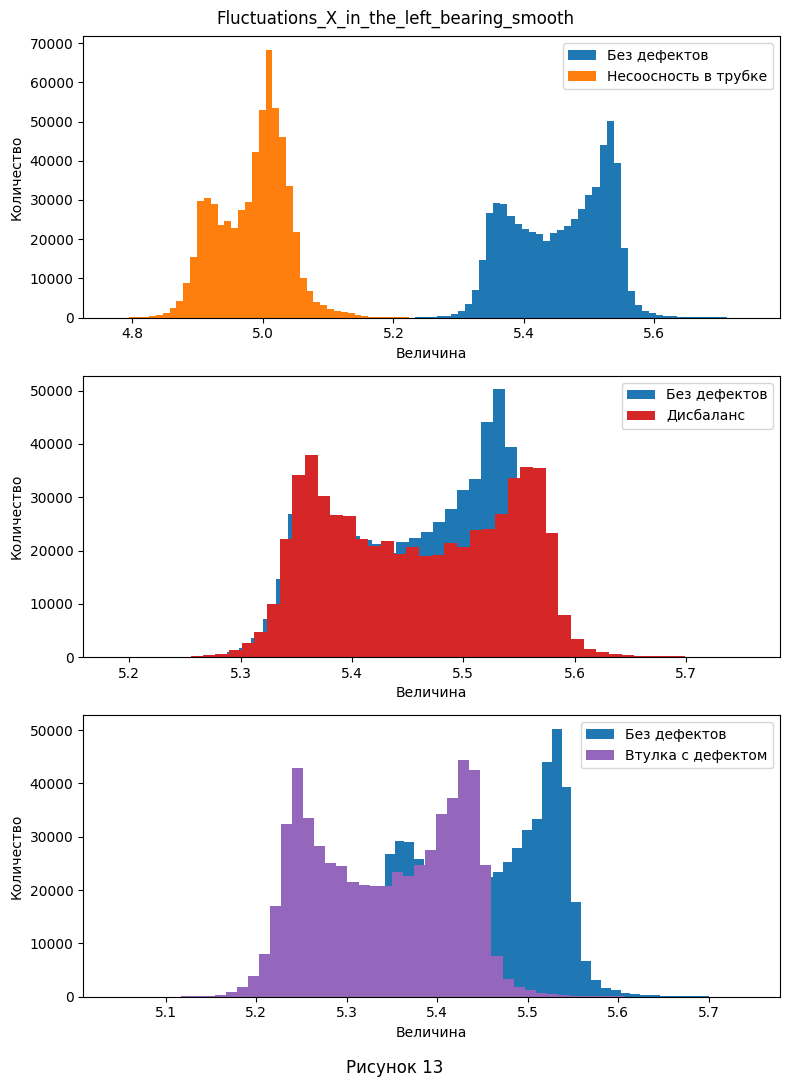
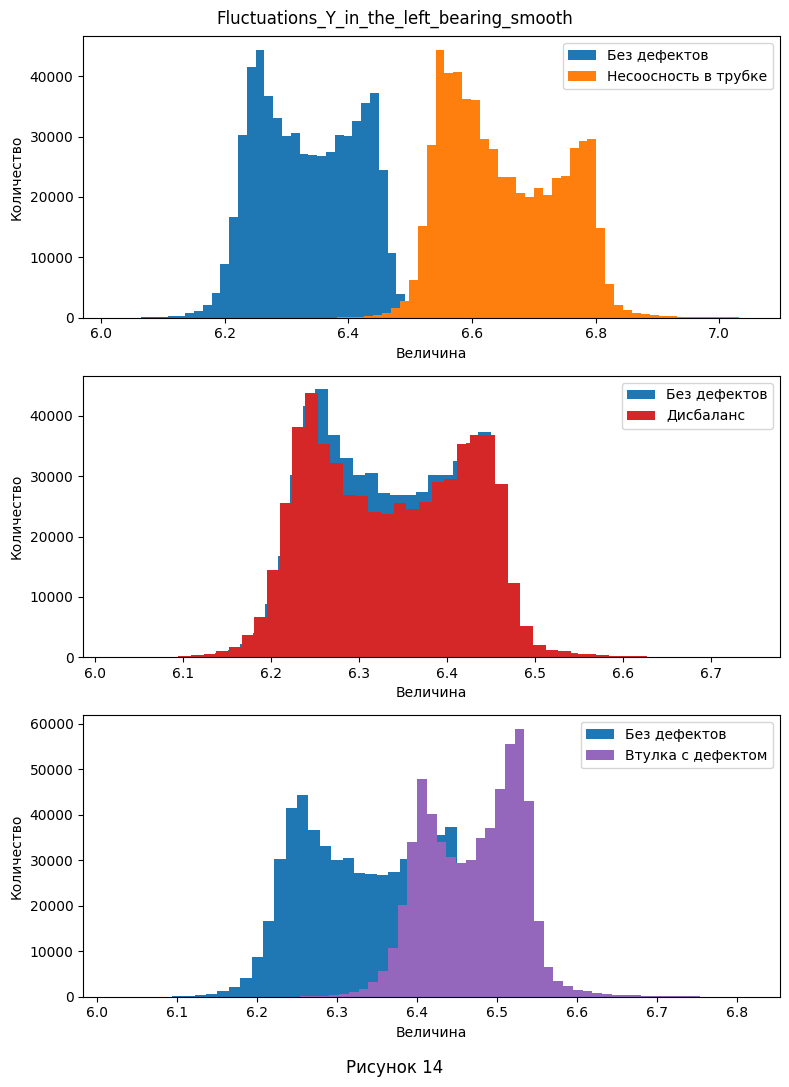
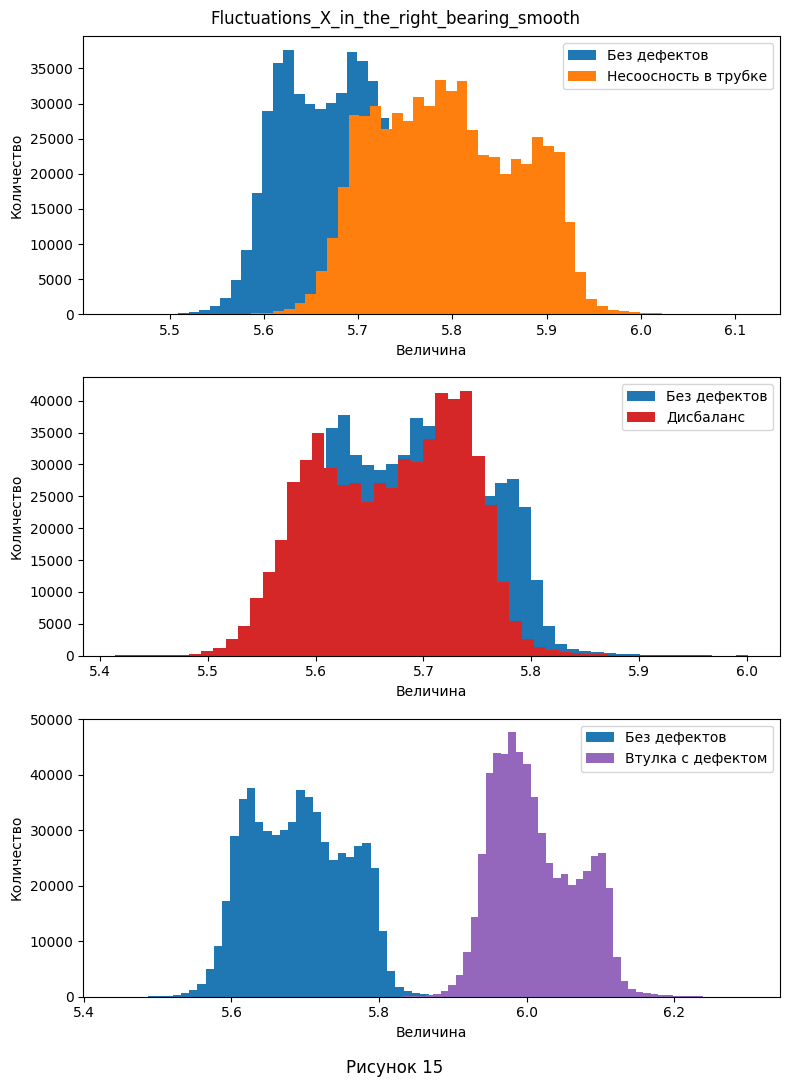
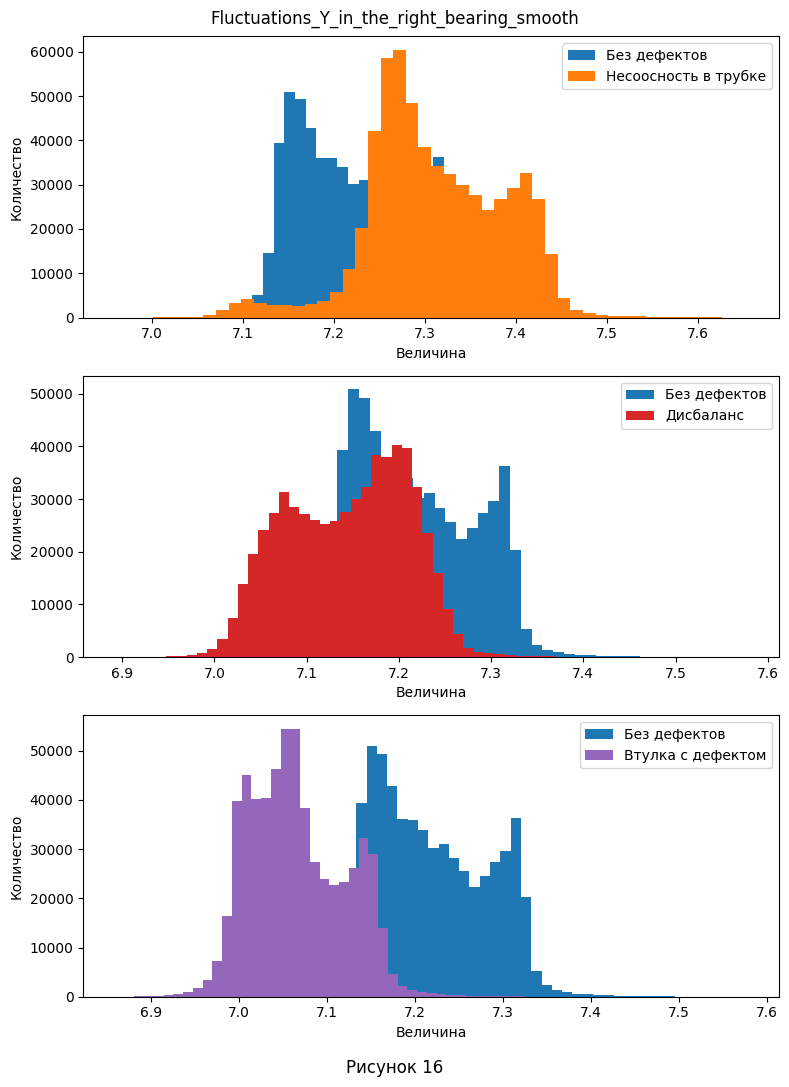
- Из визуализации видно, что несглаженные данные имеют одиночные выбросы - отдельные окружности, не сливающиеся с соседними. Поэтому при дальнейшей работе есть смысл использовать сглаженные данные, так как они дают более широкую гистаграмму, чем позволяют лучше видеть диапазон принимаемых значений и уменьшают количество выбросов. Так же сгруппируем графики по параметрам колонок 5-8. На каждом графике изобразим одновременно распределение с и без дефектов. Заметим, что нам не так уж важны конкретные значения, поэтому, для урупнения изображений было принято решение не делать общей шкалу величины.
for i, field in enumerate(df_norm.keys()[4:-2]):
fig, ax = plt.subplots(3, 1, figsize=a4figsize)
fig.suptitle(field)
fig.supxlabel(f"Рисунок {next(pic_n_gen)}")
for j, df in enumerate(dfs[1:]):
ax[j].hist(df_norm[field], bins=50, label=df_names[0], color=df_colors[0])
ax[j].hist(df[field], bins=50, label=df_names[j+1], color=df_colors[j+1])
ax[j].set_xlabel("Величина")
ax[j].set_ylabel("Количество")
ax[j].legend()
fig.tight_layout()
- Из построенной визуализации уже можно сделать некоторые выводы о том, какие признаки меняются при определённых дефектах.
-
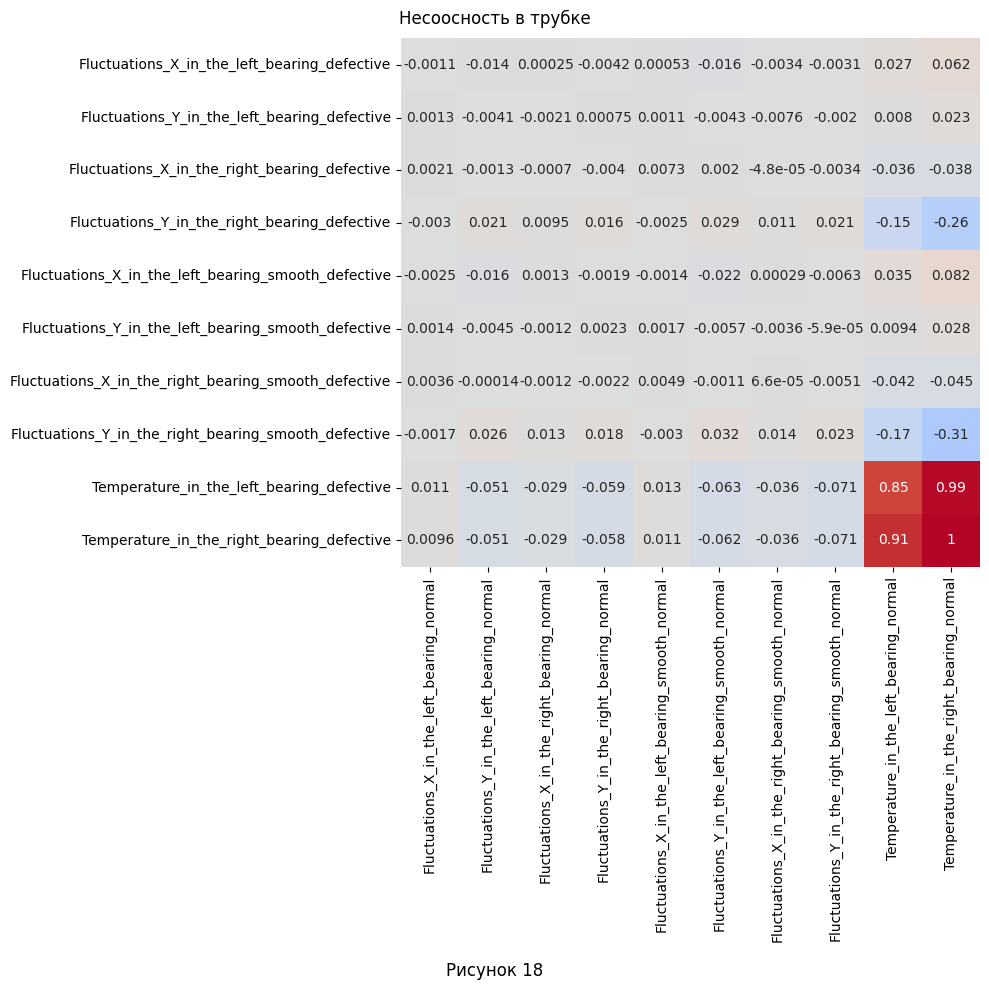
Например, видно, что при несоосности в трубке, значительные отклонения по величине наблюдаются в левом подшипнике, в то время когда в правом смещение видно в меньшей степени.
-
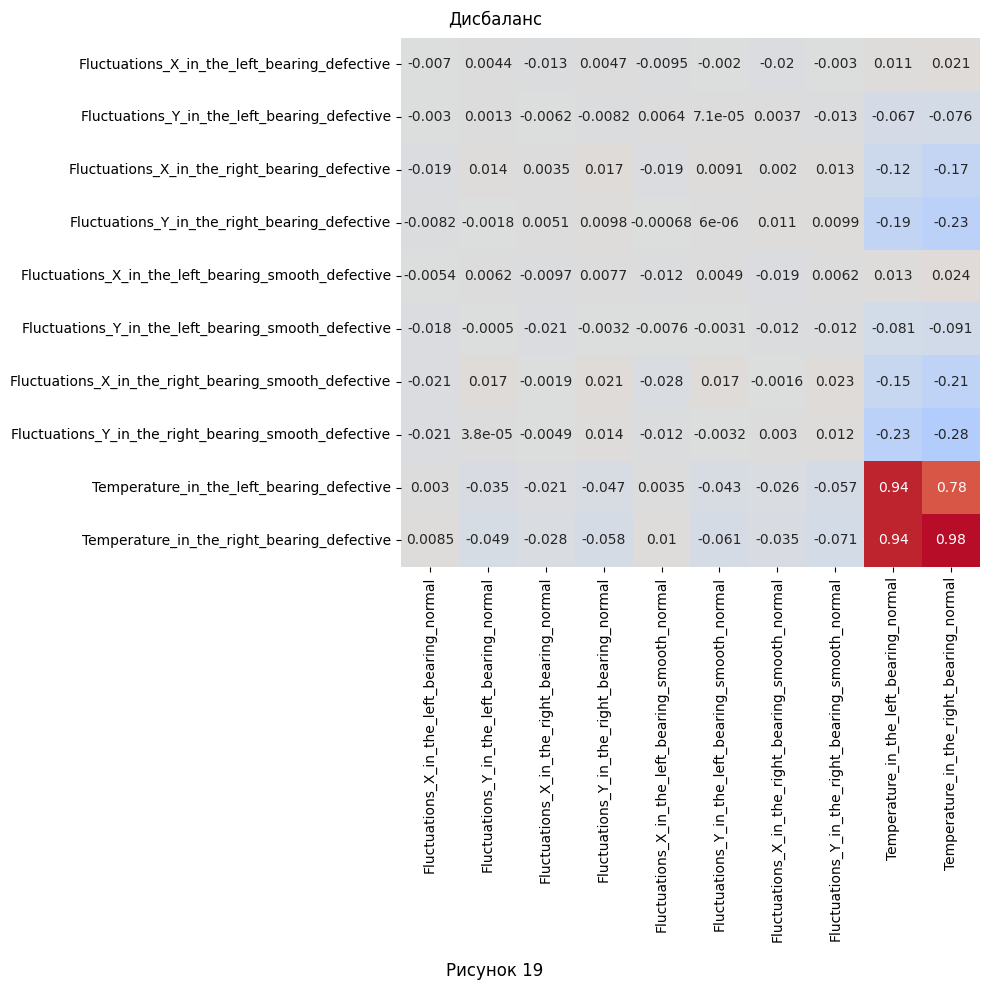
При дисбалансе, отклонения по форме и величине распределения видны только по оси Y в правом подшипнике, а остальные параметры практически совпадают.
-
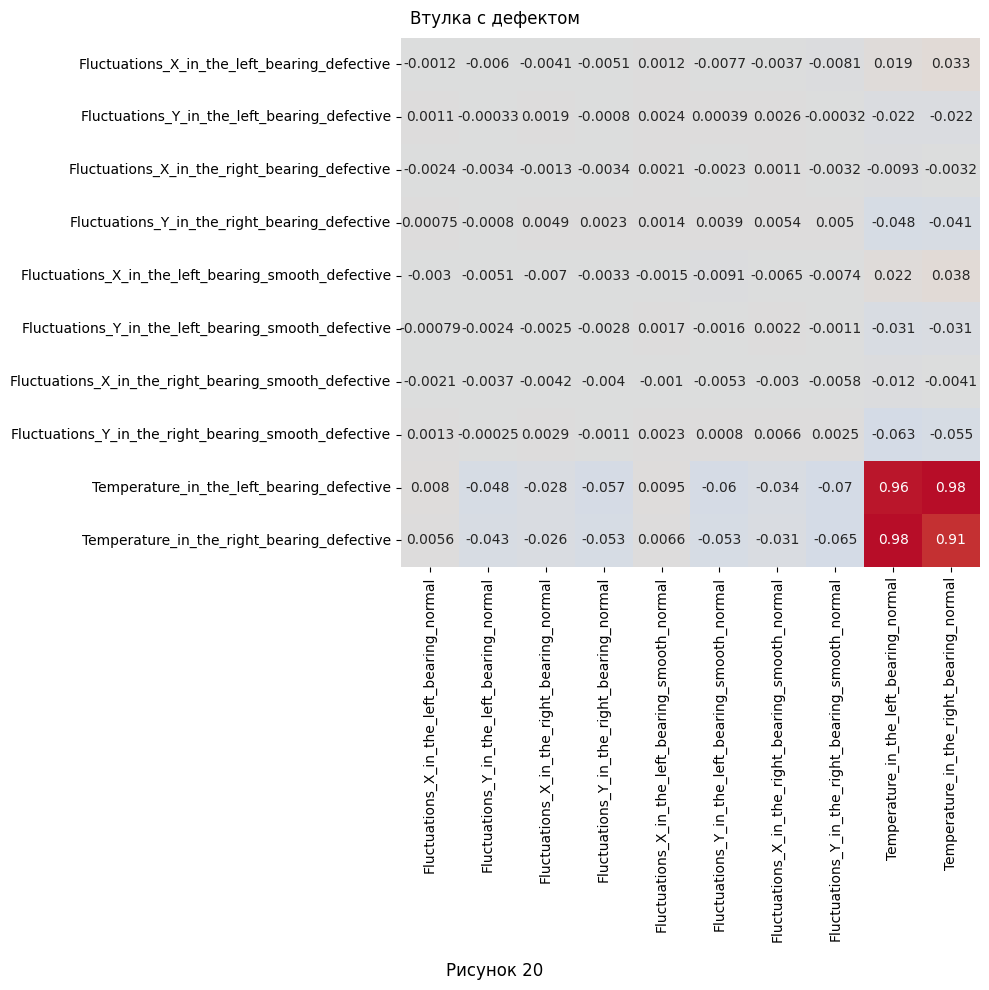
Если же проблема в дефектах втулки, тогда все параметры смещаются в большую или меньшую сторону, при этом сохраняя в общих чертах свою форму, не считая оси X в правом подшипнике.
Линейный анализ температуры
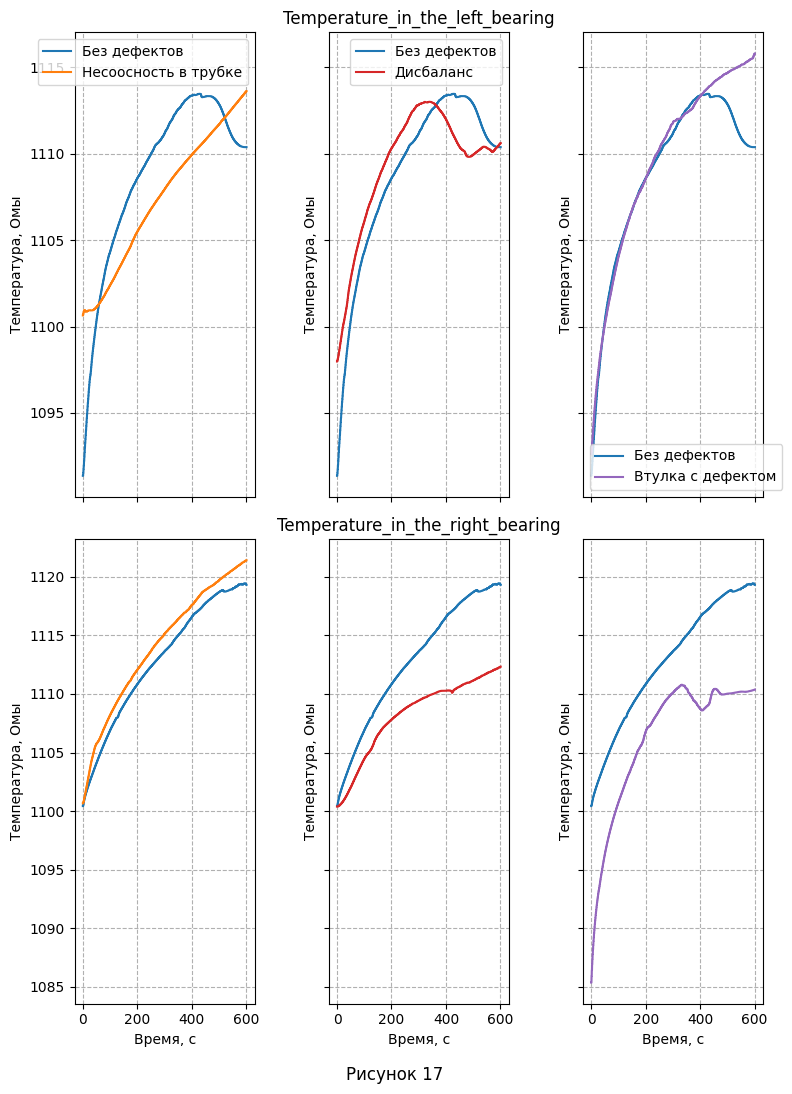
- Теперь перейдём к анализу температуры подшипников. Для этого снова изобразим линейные графики для каждого дефекта, наложив на них соответствующие значения для нормы.
fig, ax = plt.subplots(2, 3, figsize=a4figsize, sharex=True, sharey='row')
# fig.suptitle(df_names[i+1])
fig.supxlabel(f"Рисунок {next(pic_n_gen)}")
for i, df in enumerate(dfs[1:]):
for j, field in enumerate(df.keys()[-2:]):
ax[j][i].plot(time, df_norm[field], color=df_colors[0], label=df_names[0])
ax[j][i].plot(time, df[field], color=df_colors[i+1], label=df_names[i+1])
if i == 1:
ax[j][i].set_title(field)
ax[j][i].set_ylabel("Температура, Омы")
ax[j][i].grid(linestyle='--')
ax[0][i].legend()
ax[-1][i].set_xlabel("Время, с")
fig.tight_layout()
- Если смотреть на график температуры прибора без дефектов, можно увидеть обвал, начавшийся для левого подшипника на 400-ой секунде, а для правого на 500-ой. Однако, неизвестно, остановился ли рост температуры после этого, поэтому судить об окончании перехожного процесса непросто. При этом, даже если считать, что первые 400 секунд система для левой и 500 для правой входила в режим работы, ввиду однородности флуктуаций, что видно на рис. 1,3,5,7, те выводы, что были сделаны для их распределения в пункте 8, остаются в силе. Что каается температуры, на основании её изменения, так же можно сделать некоторые наблюдения:
-
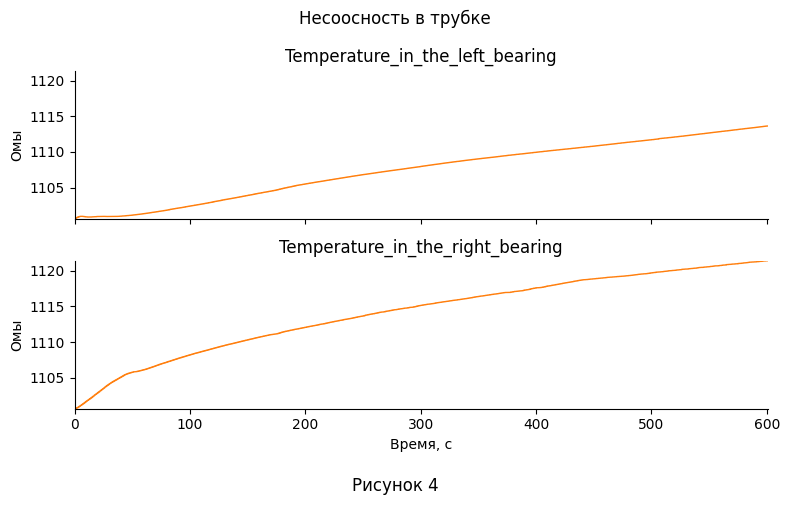
При несоосности в трубке, на левом подшипнике наблюдается более линейно растущий график, при этом около 500-ой секунды он пересекает нормальный график и не останавливает свой рост. Температура для правого несколько больше на всём временном отрезке и также не замедляет рост после 500-ой секунды
-
Дисбаланс характеризуется более высокими температурами, но при этом более коротким переходным режимом на левом подшипнике. При этом, на правом температура наоборот значительно ниже, что так же видно с самого начала наблюдений.
-
Дефектная втулка выдаёт себя только на правом подшипнике - опять же, более низкими температурами на правом подшипнике. Но, возможно, это происходит из-за гораздо более низкой начальной температуры (это можно отнести к ошибкам измерения). При этом, температурная кривая для левого подшипника практически идеально повторяет нормальную, но только до конца переходного процесса, после чего продолжает расти несмотря на его конец.
Матрица корреляции
- Наконец, построим матрицу корреляции для выявления корреляции между параметрами нормальных и имеющими дефекты наборами. Нам не интересна внутренняя корреляция, поэтому берём только корреляцию между разными наборами.
for i, df in enumerate(dfs[1:]):
fig, ax = plt.subplots(figsize=(10,10))
df_j = df.join(df_norm, lsuffix="_defective", rsuffix="_normal")
corr = df_j.corr()
corr = corr[filter(lambda key: key.count("_normal"), corr.keys())]
corr = corr[np.array(list(map(lambda key: key.count("_defective") == 1, corr.index)),dtype=bool)]
sns.heatmap(
corr,
cbar=False,
ax=ax,
annot=True,
cmap='coolwarm',
vmin=-1,
vmax=1
)
fig.suptitle(df_names[i+1])
fig.supxlabel(f"Рисунок {next(pic_n_gen)}")
fig.tight_layout()
Таблица. Критерии оценки визуализации, и примерные вопросы для их оценивания
| Вопрос | Ответ |
|---|---|
| 1.Для каждого параметра определен тип, и в зависимости его типа представлены различные описательные статистики. | В каждом наборе имеются по 10 параметров вещественного типа (float64): Fluctuations_X_in_the_left_bearing, Fluctuations_Y_in_the_left_bearing, Fluctuations_X_in_the_right_bearing, Fluctuations_Y_in_the_right_bearing, Fluctuations_X_in_the_left_bearing_smooth, Fluctuations_Y_in_the_left_bearing_smooth, Fluctuations_X_in_the_right_bearing_smooth, Fluctuations_Y_in_the_right_bearing_smooth, Temperature_in_the_left_bearing, Temperature_in_the_right_bearing. В файле ipynb в пункте 2 представлены в табличном виде некоторые описательные характеристики этих полей для каждого из наборов данных, такие как количество элементов 601000, среднее, стандартное отклонение, минимум и максимум, 25% и 75% квартили, медиана. Из графиков на рис. 1-8 видно, что линейное представление флуктуаций несёт мало информации, поэтому в дальнейшем будут исследоваться только распределение (рис. 13-16) и корреляция (рис. 18-20) между этими признаками. С другой стороны, график температуры имеет ясно различимую временную зависимость, поэтому для него имеет смысл рассмотреть её (рис. 17), а так же корреляцию (рис. 18-20). |
| 2. Есть ли выбросы в данных. Если да, укажите в каких атрибутах. | Из рис. 9-12 видно, что несглаженные данные имеют одиночные выбросы - отдельные окружности, не сливающиеся с соседними. - Fluctuations_X_in_the_left_bearing для несоосности в трубке, дисбаланса и втулки с дефектом - Fluctuations_Y_in_the_left_bearing для несоосности в трубке и втулке с дефектом - Fluctuations_X_in_the_right_bearing для без дефекта, несоосности в трубке, дисбаланса и втулки с дефектом - Fluctuations_Y_in_the_right_bearing для без дефекта, несоосности в трубке, дисбаланса и втулки с дефектом Поэтому при дальнейшей работе есть смысл использовать сглаженные данные, так как они дают более широкую гистаграмму, чем позволяют лучше видеть диапазон принимаемых значений и уменьшают количество выбросов. |
| 3. Есть ли переходный период, в течение которой система выходит на режим. Если да, укажите его длительность (можно указать число записей, которые описывают этот переходный период). |
Если смотреть на график температуры прибора без дефектов (рис. 17), можно увидеть обвал, начавшийся для левого подшипника на 400-ой секунде, а для правого на 500-ой. Однако, неизвестно, остановился ли рост температуры после этого, поэтому судить об окончании перехожного процесса непросто. |
| 4. Определите, какие атрибуты наиболее сильно отличаются в экспериментах с дефектами, от нормальных значений. | Из построенной визуализации на рис. 13-16 для распределения флуктуаций: - Видно, что при несоосности в трубке, значительные отклонения по величине наблюдаются в левом подшипнике, в то время когда в правом смещение видно в меньшей степени. - При дисбалансе, отклонения по форме и величине распределения видны только по оси Y в правом подшипнике, а остальные параметры практически совпадают. - Если же проблема в дефектах втулки, тогда все параметры смещаются в большую или меньшую сторону, при этом сохраняя в общих чертах свою форму, не считая оси X в правом подшипнике. Из графиков для температуры (рис. 19) - При несоосности в трубке, на левом подшипнике наблюдается более линейно растущий график, при этом около 500-ой секунды он пересекает нормальный график и не останавливает свой рост. Температура для правого несколько больше на всём временном отрезке и также не замедляет рост после 500-ой секунды. - Дисбаланс характеризуется более высокими температурами, но при этом более коротким переходным режимом на левом подшипнике. При этом, на правом температура наоборот значительно ниже, что так же видно с самого начала наблюдений. - Дефектная втулка выдаёт себя только на правом подшипнике - опять же, более низкими температурами на правом подшипнике. Но, возможно, это происходит из-за гораздо более низкой начальной температуры (это можно отнести к ошибкам измерения). При этом, температурная кривая для левого подшипника практически идеально повторяет нормальную, но только до конца переходного процесса, после чего продолжает расти несмотря на его конец. |
| 5. Можно ли на этапе переходного периода говорить о наличии дефекта? Какие признаки на это могут указывать? | Если считать, что первые 400 секунд система для левой и 500 для правой входила в режим работы, ввиду однородности флуктуаций, что видно на рис. 1,3,5,7, те выводы, что были сделаны для их распределения в предыдущем вопросе, остаются в силе. Не считая тех частей кривых температур (рис. 17), которые лежат дальше 500 с: - При несоосности в трубке, на левом подшипнике, около 500-ой секунды график пересекает нормальный график и не останавливает свой рост. Температура для также не замедляет рост после 500-ой секунды. - У дефектной втулки температурная кривая для левого подшипника по окончанию переходного процесса, после чего продолжает расти несмотря на его конец. |