Студент гр. 1181 |
|
Шишков Д.А. |
Преподаватель |
|
Ситникова М.Ф. |
No ВАР. |
Элемент |
Структура |
Атомная масса |
Параметр решетки, Å |
Плотность, г/см3 |
Удельное сопротивление, мкОм·см |
Температура, К |
Работа выхода φ, эВ |
||
Дебая (TD) |
Ферми (TF·10-4) |
плавления (Tпл) |
||||||||
14 |
Au |
ГЦК |
196.9 |
4.08 |
19.28 |
2.2 |
165 |
6.39 |
1337 |
4.58 |
№ ВАР. |
Тип примеси |
Полупроводник |
Ширина запрещённой области |
Эффективная масса |
Подвижность при 300К |
Работа выхода, Эв |
||
EG (300 К), Эв |
m"n/me |
m’’p/me |
μn, см2·В1·с1 |
μp, см2·В1·с1 |
||||
6 |
n |
InSb |
0.17 |
0.0133 |
0.6 |
76000 |
5000 |
4.75 |
№ вар. |
3 |
концентрация примесей, м-3 |
1022 |
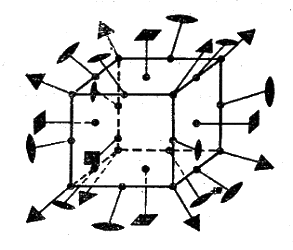 Рис. 1 Изображение осей симметрии кубической решётки
Рис. 1 Изображение осей симметрии кубической решётки
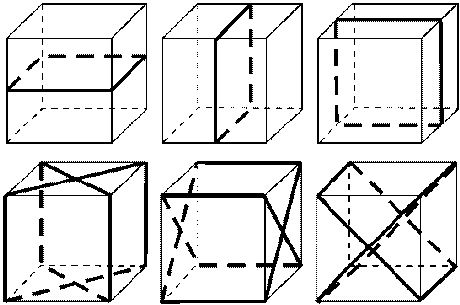 Рис. 2 Изображение плоскостей симметрии куба
Рис. 2 Изображение плоскостей симметрии куба
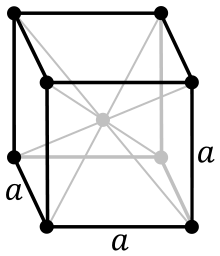 Рис. 3 Изображение центра симметрии куба
Базисные вектора:
Рис. 3 Изображение центра симметрии куба
Базисные вектора:
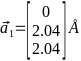 ,
, 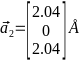 ,
, 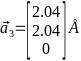 Кристаллическая решётка по заданным векторам построена на рис. 4
Кристаллическая решётка по заданным векторам построена на рис. 4
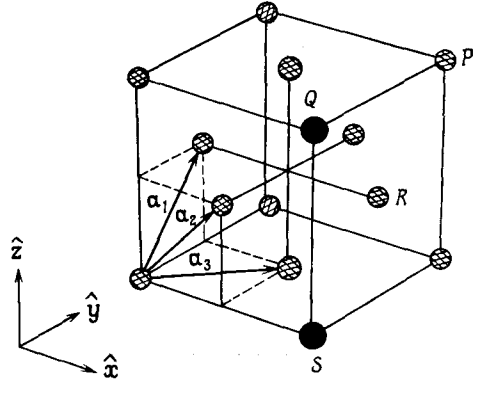 Рис. 4 Тройка основных векторов для ГЦК решётки
Объём элементарной ячейки:
Рис. 4 Тройка основных векторов для ГЦК решётки
Объём элементарной ячейки:
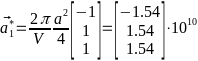 ,
, 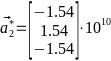 ,
, 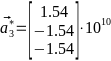 Что соответствует ОЦК. Её изображение на рис. 5.
Что соответствует ОЦК. Её изображение на рис. 5.
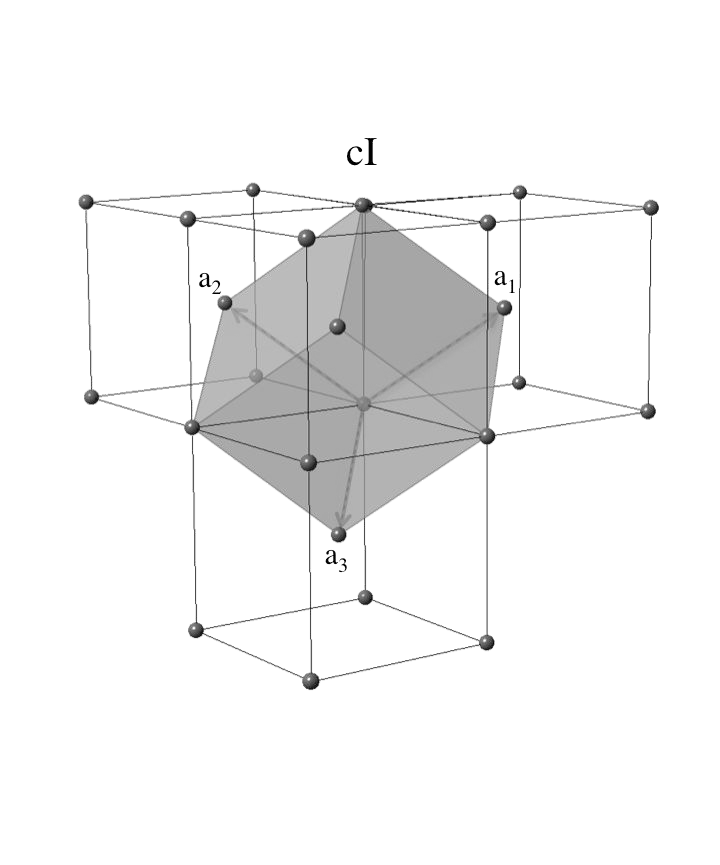 Рис. 5 Обратная решётка для ГЦК — ОЦК
Первая зона Бриллюэна (рис. 6):
Рис. 5 Обратная решётка для ГЦК — ОЦК
Первая зона Бриллюэна (рис. 6):
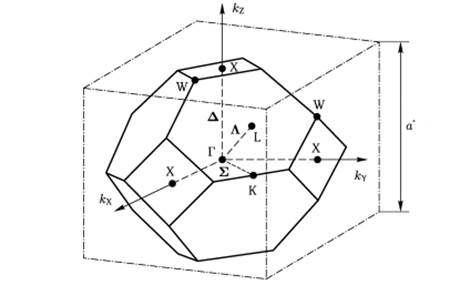 Рис. 6 Первая зона Бриллюэна
Размеры зоны Бриллюэна по направлениям X, L, K:
Рис. 6 Первая зона Бриллюэна
Размеры зоны Бриллюэна по направлениям X, L, K:
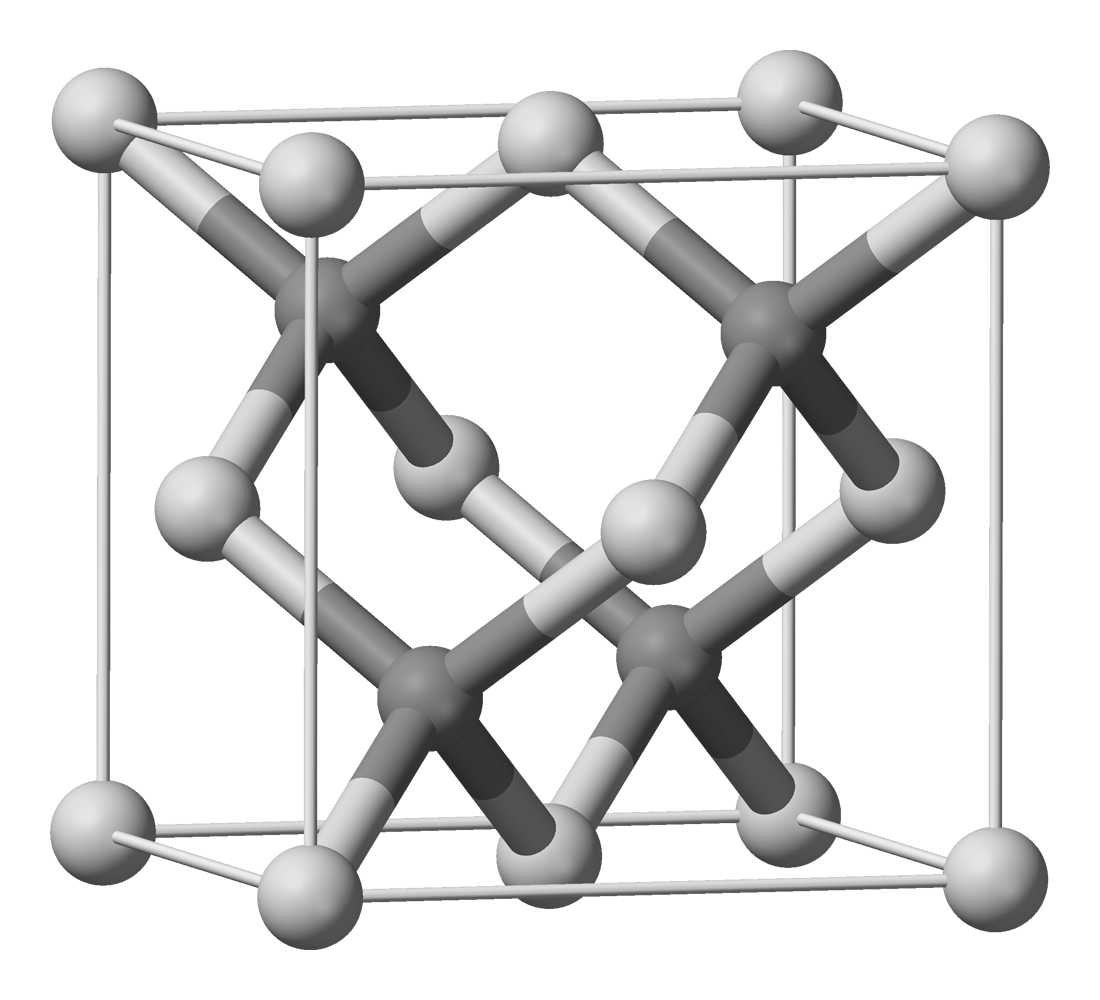 Рис. 7 Антимонид индия
Структура: Гранецентрированная кубическая решётка
Формула симметрии: 3L44L36L29PC
Класс симметрии: m3m
Изображения осей, плоскостей и центра симметрии для последнего — см.
рис. 1-3.
Базисные вектора:
Рис. 7 Антимонид индия
Структура: Гранецентрированная кубическая решётка
Формула симметрии: 3L44L36L29PC
Класс симметрии: m3m
Изображения осей, плоскостей и центра симметрии для последнего — см.
рис. 1-3.
Базисные вектора:
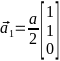 ,
, 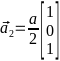 ,
, 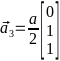 , считая, что постоянная решётки
= 1
Для параметра решётки
, считая, что постоянная решётки
= 1
Для параметра решётки 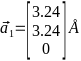 ,
, 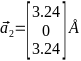 ,
, 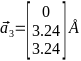 Кристаллическая решётка по заданным векторам изображена на рис. 4.
Объём элементарной ячейки аналогично предыдущему пункту:
Кристаллическая решётка по заданным векторам изображена на рис. 4.
Объём элементарной ячейки аналогично предыдущему пункту:
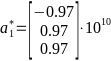 ,
, 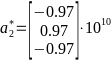 ,
, 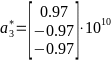 # 2) Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов.
Связь радиуса Ферми с концентрацией электронов можно выяснить из
следующего выражения:
# 2) Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов.
Связь радиуса Ферми с концентрацией электронов можно выяснить из
следующего выражения:  Рис. 8 Атомы элементарной ячейки ГЦК решётки
При Z = 1
Рис. 8 Атомы элементарной ячейки ГЦК решётки
При Z = 1 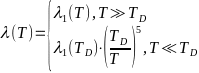 .
Где
.
Где 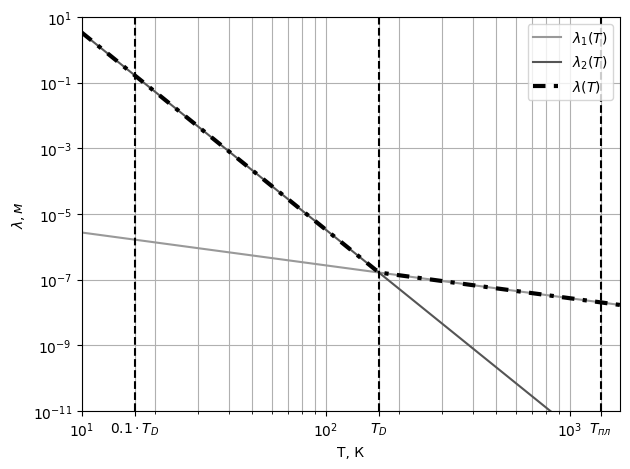 Рис. 9 График зависимости длин свободного пробега от температуры
*Вывод:* с ростом температуры длина свободного пробега действительно
уменьшается.
## 3.2) Исследование влияния дефектов на время релаксации
Время релаксации для рассеивания на дефектах:
Рис. 9 График зависимости длин свободного пробега от температуры
*Вывод:* с ростом температуры длина свободного пробега действительно
уменьшается.
## 3.2) Исследование влияния дефектов на время релаксации
Время релаксации для рассеивания на дефектах: 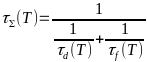 .
Оно справедливо если
один
из
механизмов рассеяния
преобладает
над другим
при
*T *=
273 *К*.
.
Оно справедливо если
один
из
механизмов рассеяния
преобладает
над другим
при
*T *=
273 *К*.
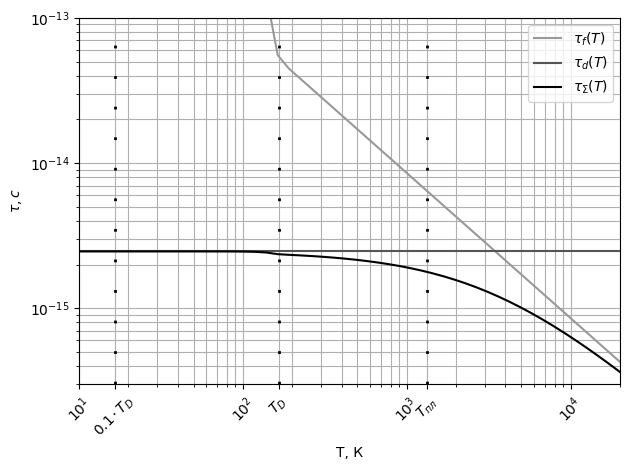 Рис. 10 График зависимости времени релаксации
от
температуры
Для разных температур и времён релаксации для рассеяния на дефектах вычислим общее время релаксации
по
правилу
Маттиссена:
*Таблица 4. Суммарное время релаксации
Рис. 10 График зависимости времени релаксации
от
температуры
Для разных температур и времён релаксации для рассеяния на дефектах вычислим общее время релаксации
по
правилу
Маттиссена:
*Таблица 4. Суммарное время релаксации
|
|
TD |
Tпл |
10-12 |
10-12 |
|
|
10-13 |
10-13 |
|
|
10-14 |
10-14 |
|
|
|
|
TD |
Tпл |
10-12 |
|
|
|
10-13 |
|
|
|
10-14 |
|
|
|
|
|
TD |
Tпл |
10-12 |
|
|
|
10-13 |
805 |
|
|
10-14 |
80.5 |
675 |
|
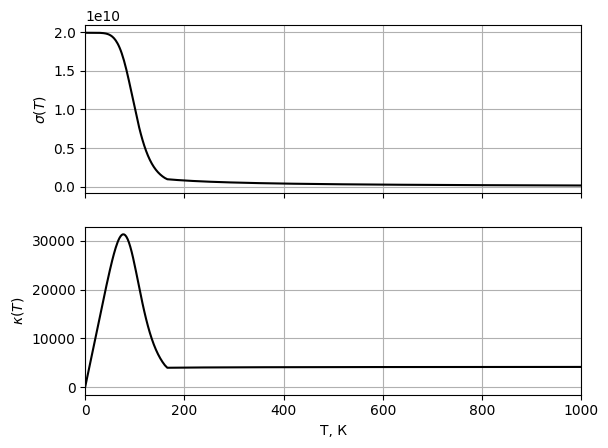 Рис. 11
Графики
зависимости электропроводности и
теплопроводности при
Рис. 11
Графики
зависимости электропроводности и
теплопроводности при 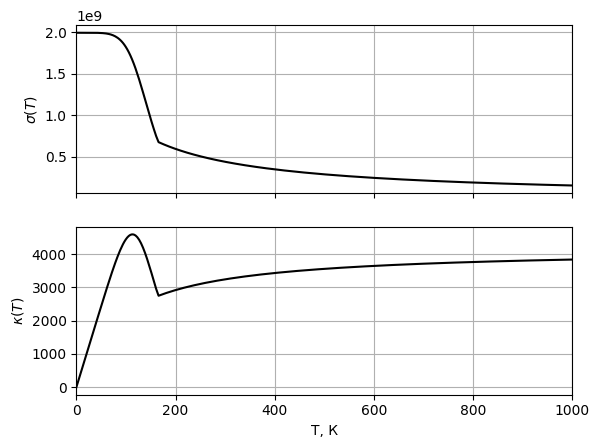 Рис. 12 Графики
зависимости электропроводности и
теплопроводности при
Рис. 12 Графики
зависимости электропроводности и
теплопроводности при 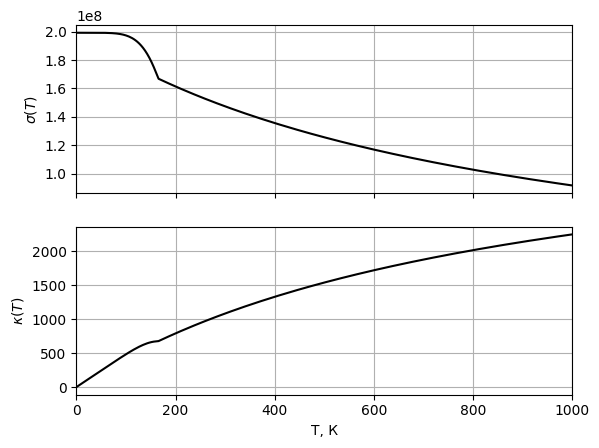 Рис. 13 Графики
зависимости электропроводности и
теплопроводности при
Рис. 13 Графики
зависимости электропроводности и
теплопроводности при 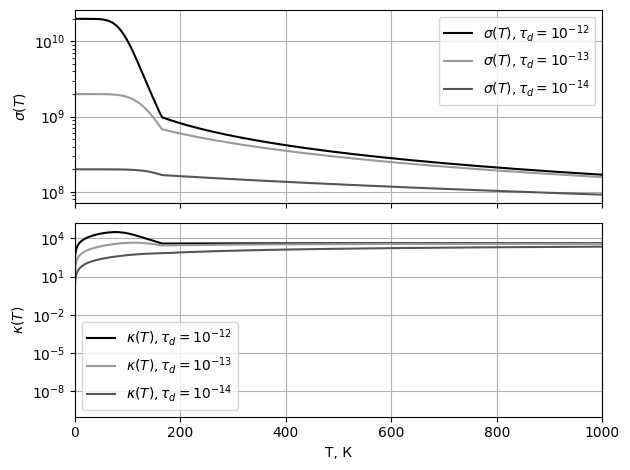 Рис. 14 Графики электропроводностей и теплопроводностей
при различных
Рис. 14 Графики электропроводностей и теплопроводностей
при различных 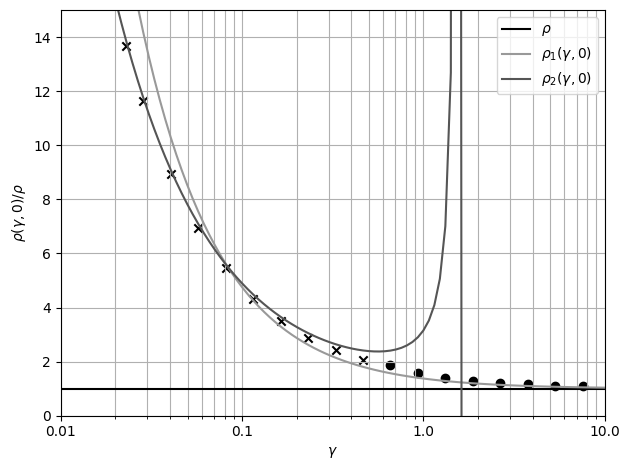 Рис. 15 График удельного сопротивления от толщины плёнки при параметре
зеркальности 0
Рис. 15 График удельного сопротивления от толщины плёнки при параметре
зеркальности 0
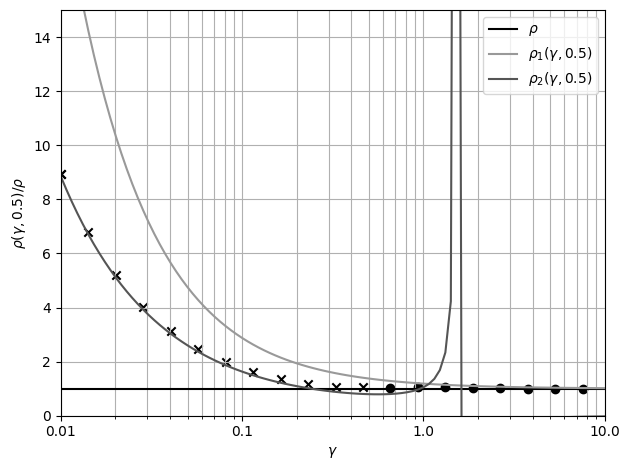 Рис. 16 График удельного сопротивления от толщины плёнки при параметре
зеркальности 0.5
При p = 1 (весь импульс электрона по направлению тока сохраняется),
размерный эффект отсутствует
Минимальную возможную толщину металлизации можно определить из
вышеприведённых графиков, выбрав такую
Рис. 16 График удельного сопротивления от толщины плёнки при параметре
зеркальности 0.5
При p = 1 (весь импульс электрона по направлению тока сохраняется),
размерный эффект отсутствует
Минимальную возможную толщину металлизации можно определить из
вышеприведённых графиков, выбрав такую 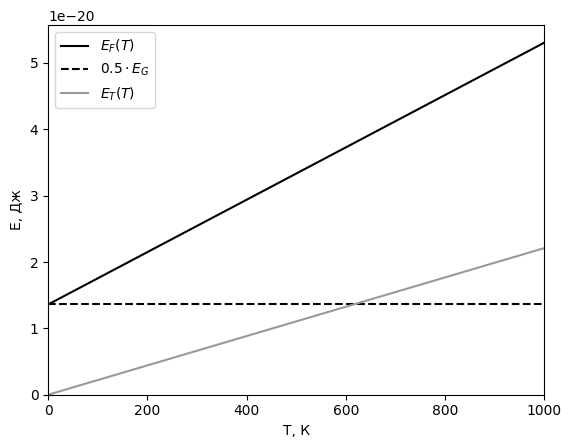 Рис. 17 График температурной зависимости энергии Ферми и тепловой
энергии
Как видно из графика, критерий вырожденности
Рис. 17 График температурной зависимости энергии Ферми и тепловой
энергии
Как видно из графика, критерий вырожденности 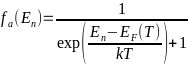 . Например, для
. Например, для 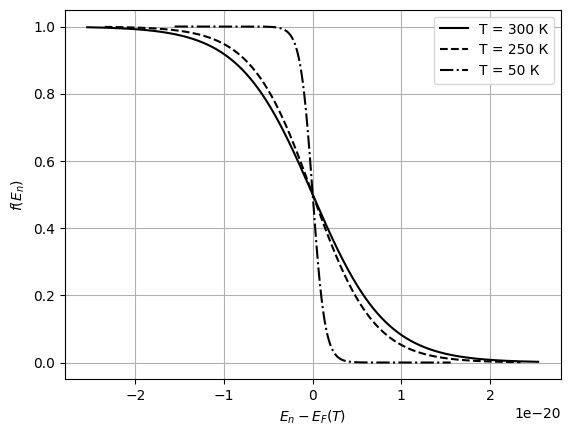 Рис. 18 Распределение Ферми-Дирака носителей заряда по энергиям при
Рис. 18 Распределение Ферми-Дирака носителей заряда по энергиям при 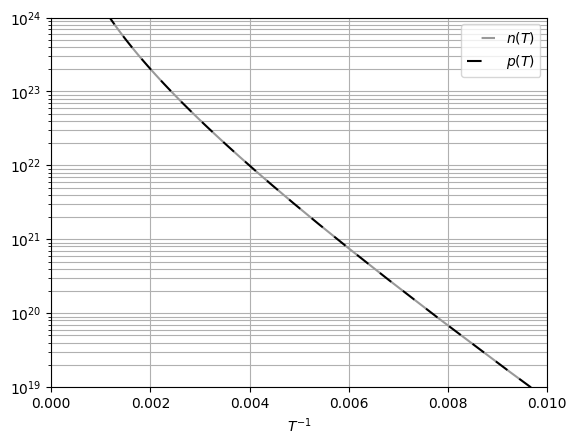 Рис. 19 График зависимостей концентрации электронов и дырок от
температуры
## 5.4) Исследование зависимости концентрации носителей заряда от температуры для примесного полупроводника
В работе рассмотрена донорная примесь Te с энергией ионизации в
кристаллической решётке антимонида индия *E**g* =
*E**d* = 0.003 *эВ*. Её концентрация *N**d* =
1022 *м*-3.
Тогда, концентрация электронов в ней равна
Рис. 19 График зависимостей концентрации электронов и дырок от
температуры
## 5.4) Исследование зависимости концентрации носителей заряда от температуры для примесного полупроводника
В работе рассмотрена донорная примесь Te с энергией ионизации в
кристаллической решётке антимонида индия *E**g* =
*E**d* = 0.003 *эВ*. Её концентрация *N**d* =
1022 *м*-3.
Тогда, концентрация электронов в ней равна 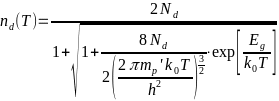 Кроме этого, справедливы аппроксимации:
Кроме этого, справедливы аппроксимации:
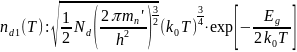
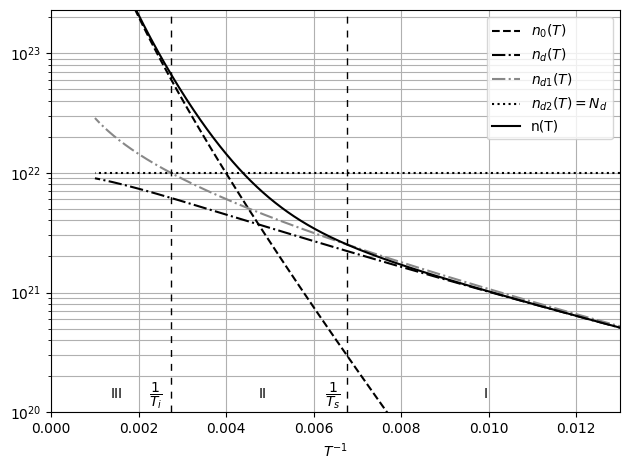 Рис. 20 График зависимости концентрации зарядов в примесном проводнике
от обратной температуры
Рис. 20 График зависимости концентрации зарядов в примесном проводнике
от обратной температуры
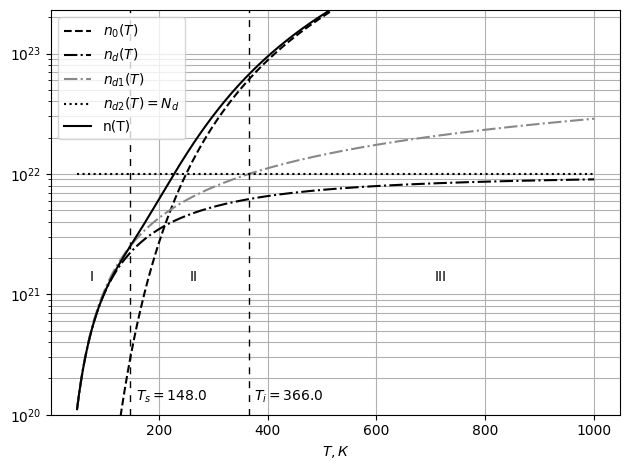 Рис. 21 График зависимости концентрации зарядов в примесном проводнике
от температуры
По графику определяются температуры перехода к собственной проводимости
и истощения примесей: *T**s* = 148 *К* (точка пересечения
*n**d*1(*T*) и *n*(*T*)) и *T**i* = 366 *К*
(момент, когда *n**d1*(*T*) становится больше Nd).
Таким образом, I — область примесной ионизации, II — область истощения,
III — область собственной ионизации.
## 5.5) Исследование зависимости подвижности от температуры для примесного полупроводника
Аппроксимирующие выражения для электронной и дырочной проводимостей:
Рис. 21 График зависимости концентрации зарядов в примесном проводнике
от температуры
По графику определяются температуры перехода к собственной проводимости
и истощения примесей: *T**s* = 148 *К* (точка пересечения
*n**d*1(*T*) и *n*(*T*)) и *T**i* = 366 *К*
(момент, когда *n**d1*(*T*) становится больше Nd).
Таким образом, I — область примесной ионизации, II — область истощения,
III — область собственной ионизации.
## 5.5) Исследование зависимости подвижности от температуры для примесного полупроводника
Аппроксимирующие выражения для электронной и дырочной проводимостей:
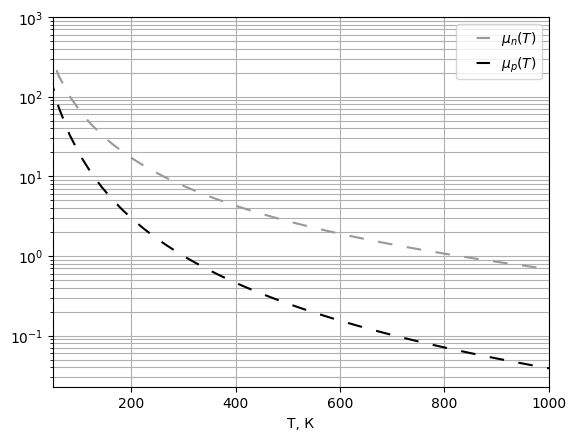 Рис. 22 График подвижностей электронов и дырок
## 5.6) Исследование зависимости электропроводности от температуры для примесного полупроводника
Электропроводность проводника выражается следующим образом:
Рис. 22 График подвижностей электронов и дырок
## 5.6) Исследование зависимости электропроводности от температуры для примесного полупроводника
Электропроводность проводника выражается следующим образом:
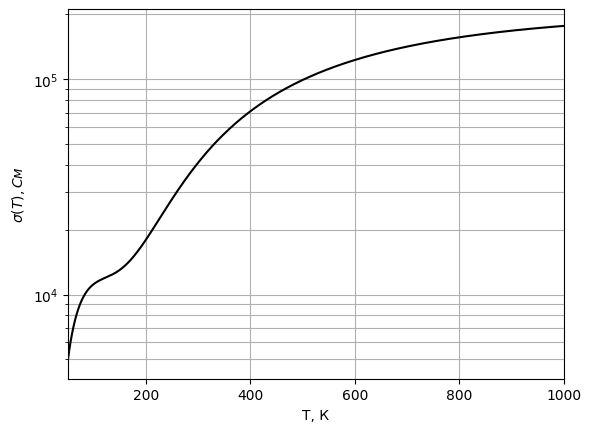 Рис. 23 График электропроводности примесного полупроводника
*Вывод*: ввиду
вырожденности, электронный газ описывается распределением Ферми-Дирака.
В собственном полупроводнике количество электронов и дырок равно,
поэтому зависимости концентраций совпадают. Добавление донорной примеси
увеличивает концентрацию электронов, однако, с ростом температуры они
истощаются и полупроводник переходит к собственной ионизации. С ростом
температуры за счёт ионизации, а значит увеличения количества носителей
заряда, в отличие от металла, проводимость полупроводника растёт.
# 6) Рассчитать зависимости энергии Ферми и термодинамической работы выхода для примесного полупроводника от температуры.
Термодинамическая работа выхода для собственного полупроводника
определяется следующим выражением:
Рис. 23 График электропроводности примесного полупроводника
*Вывод*: ввиду
вырожденности, электронный газ описывается распределением Ферми-Дирака.
В собственном полупроводнике количество электронов и дырок равно,
поэтому зависимости концентраций совпадают. Добавление донорной примеси
увеличивает концентрацию электронов, однако, с ростом температуры они
истощаются и полупроводник переходит к собственной ионизации. С ростом
температуры за счёт ионизации, а значит увеличения количества носителей
заряда, в отличие от металла, проводимость полупроводника растёт.
# 6) Рассчитать зависимости энергии Ферми и термодинамической работы выхода для примесного полупроводника от температуры.
Термодинамическая работа выхода для собственного полупроводника
определяется следующим выражением:
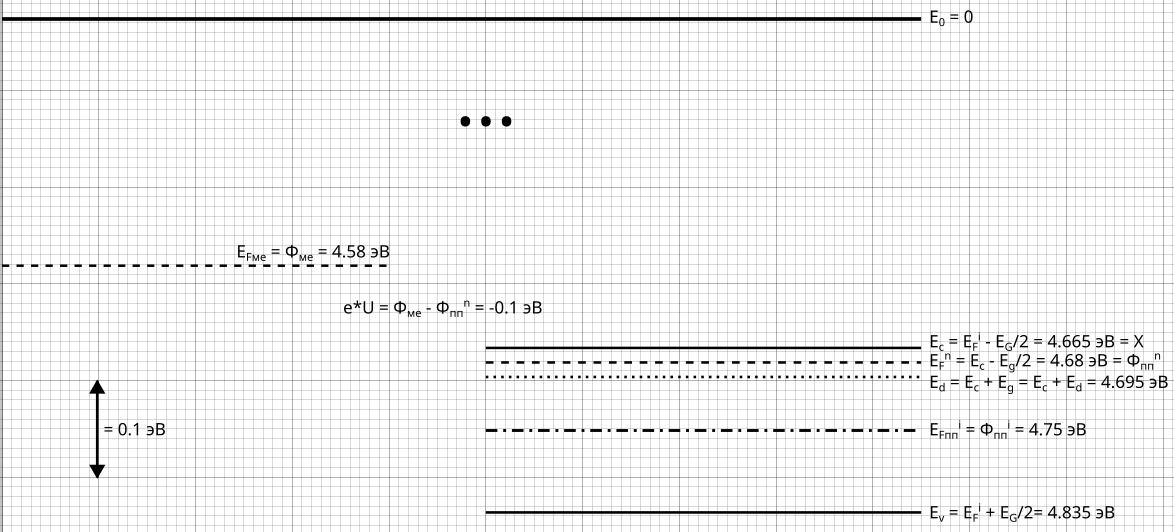 Рис. 24 Энергетическая диаграмма металл-вакуум-полупроводник
Рис. 24 Энергетическая диаграмма металл-вакуум-полупроводник
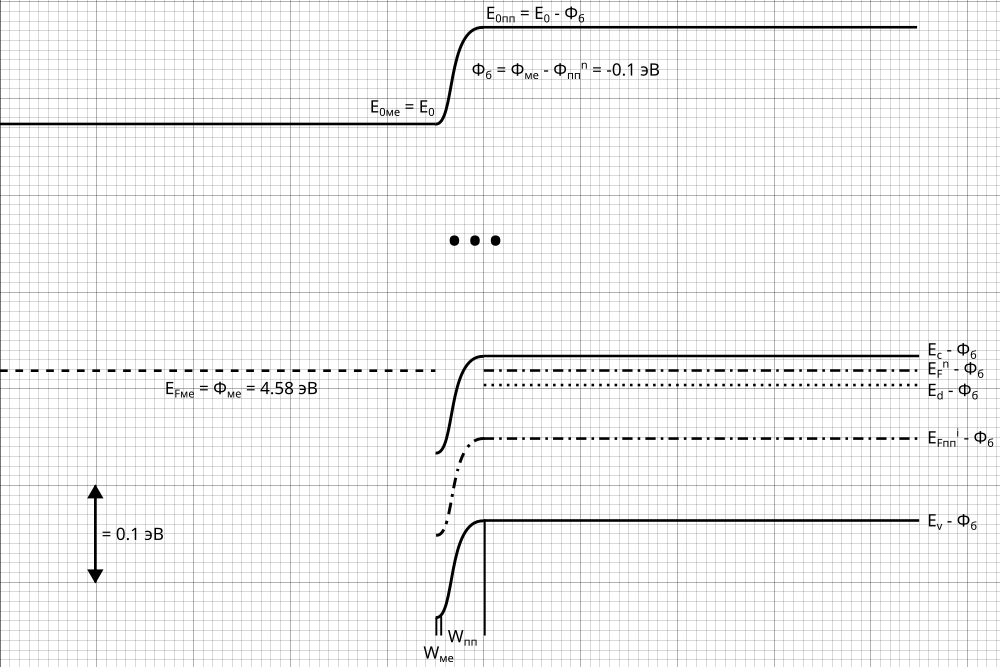 Рис. 25 Энергетическая диаграмма металл-полупроводник
Вывод: Так как
Рис. 25 Энергетическая диаграмма металл-полупроводник
Вывод: Так как 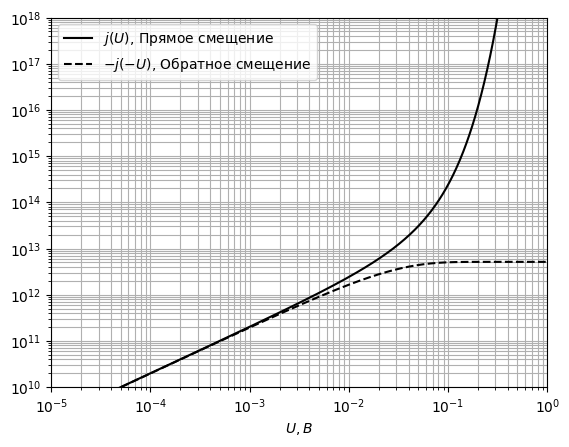 Рис. 28 ВАХ контакта при *T* = 300 *К*
Рис. 28 ВАХ контакта при *T* = 300 *К*
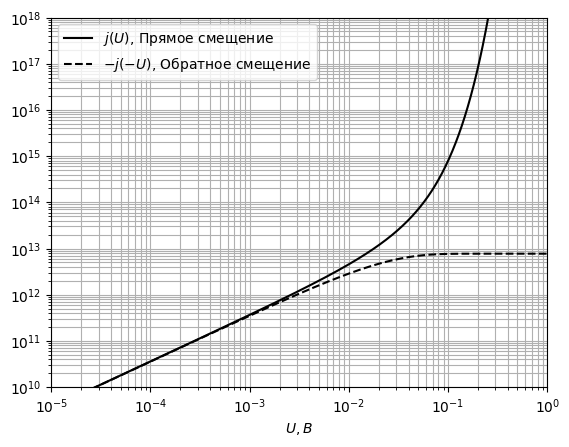 Рис. 29 ВАХ контакта при *T* = 250 *К*
Рис. 29 ВАХ контакта при *T* = 250 *К*
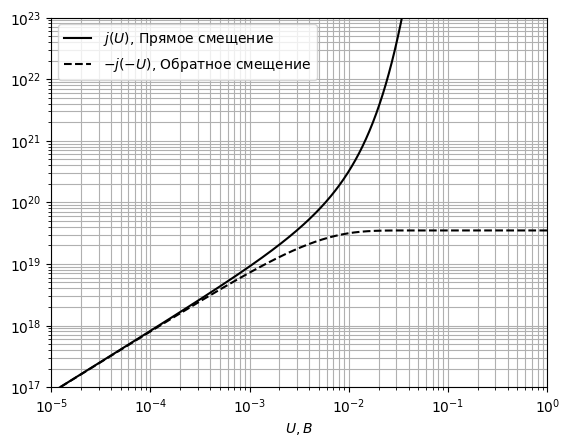 Рис. 30 ВАХ контакта при *T* = 50 *К*
Вывод: анти-барьер Шоттки виден и на ВАХ, где в области небольших напряжений выполняется
закон Ома. Сопротивление в ней определяется только сопротивлением приконтактной области полупроводника.
# 8) Рассчитать концентрацию носителей заряда в заданном полупроводнике для создания омического контакта к металлу.
Как видно из п. 7, контакт Au-InSb образует анти-барьер Шоттки, поэтому
дополнительно легированный буферный слой не требуется.
# 9) Сделать выводы и дать рекомендации по применению исследуемого контакта металл-полупроводник
В работе были исследованы металл золото (Au) и полупроводник антимонид
индия (InSb). Оба материала имеют гранецентрированную кристаллическую
решётку, характеристики каждой были исследованы в п. 1.
В п. 2 на основании вычисления концентрации свободных электронов было
выяснено, что к металлу неприменима теория свободных электронов.
Золото является хорошим проводником, что было подтверждено в п. 3, где
была исследована температурная зависимость проводимости и связанные с
ней характеристики и влияние на неё дефектов кристаллической решётки.
При этом, как показано в п. 4, при толщине менее 60 нм начинает
сказываться размерный эффект — при отражении на неровностях теряется
импульс по направлению движения электронов, из-за чего сильно возрастает
сопротивление.
В п. 5 на основании заданных эффективных масс электронов и «дырок» было
выяснено, что антимонид индия является вырожденным, а значит, должно
использоваться распределение Ферми-Дирака. Однако, далее в расчётах
использовались формулы для невырожденного случая. В собственном
полупроводнике, действительно, концентрации электронов и «дырок»
совпали.
С добавлением донорной примеси теллура (Te) при низких температурах
концентрация электронов возрастает за счёт ионизации примесей, однако,
по мере роста температуры они истощаются и уже при 366 К их вклад
становится пренебрежимо мал. Проводимость полупроводника на несколько
порядков меньше, чем у металла и возрастает по мере роста температуры.
В п. 6 было показано, что добавление примеси в полупроводник уменьшает
работу выхода.
На основании энергетических диаграмм, построенных в п. 7 было выяснено,
что золото и антимонид индия, легированных теллуром образуют омический
контакт с высотой барьера
Рис. 30 ВАХ контакта при *T* = 50 *К*
Вывод: анти-барьер Шоттки виден и на ВАХ, где в области небольших напряжений выполняется
закон Ома. Сопротивление в ней определяется только сопротивлением приконтактной области полупроводника.
# 8) Рассчитать концентрацию носителей заряда в заданном полупроводнике для создания омического контакта к металлу.
Как видно из п. 7, контакт Au-InSb образует анти-барьер Шоттки, поэтому
дополнительно легированный буферный слой не требуется.
# 9) Сделать выводы и дать рекомендации по применению исследуемого контакта металл-полупроводник
В работе были исследованы металл золото (Au) и полупроводник антимонид
индия (InSb). Оба материала имеют гранецентрированную кристаллическую
решётку, характеристики каждой были исследованы в п. 1.
В п. 2 на основании вычисления концентрации свободных электронов было
выяснено, что к металлу неприменима теория свободных электронов.
Золото является хорошим проводником, что было подтверждено в п. 3, где
была исследована температурная зависимость проводимости и связанные с
ней характеристики и влияние на неё дефектов кристаллической решётки.
При этом, как показано в п. 4, при толщине менее 60 нм начинает
сказываться размерный эффект — при отражении на неровностях теряется
импульс по направлению движения электронов, из-за чего сильно возрастает
сопротивление.
В п. 5 на основании заданных эффективных масс электронов и «дырок» было
выяснено, что антимонид индия является вырожденным, а значит, должно
использоваться распределение Ферми-Дирака. Однако, далее в расчётах
использовались формулы для невырожденного случая. В собственном
полупроводнике, действительно, концентрации электронов и «дырок»
совпали.
С добавлением донорной примеси теллура (Te) при низких температурах
концентрация электронов возрастает за счёт ионизации примесей, однако,
по мере роста температуры они истощаются и уже при 366 К их вклад
становится пренебрежимо мал. Проводимость полупроводника на несколько
порядков меньше, чем у металла и возрастает по мере роста температуры.
В п. 6 было показано, что добавление примеси в полупроводник уменьшает
работу выхода.
На основании энергетических диаграмм, построенных в п. 7 было выяснено,
что золото и антимонид индия, легированных теллуром образуют омический
контакт с высотой барьера