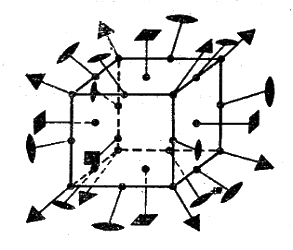
 Рис. 1 Изображение осей симметрии кубической решётки
Рис. 1 Изображение осей симметрии кубической решётки
Студент гр. 1181 |
|
Шишков Д.А. |
Преподаватель |
|
Ситникова М.Ф. |
No ВАР. |
Элемент |
Структура |
Атомная масса |
Параметр решетки, Å |
Плотность, г/см3 |
Удельное сопротивление, мкОм·см |
Температура, К |
Работа выхода φ, эВ |
||
Дебая (TD) |
Ферми (TF·10-4) |
плавления (Tпл) |
||||||||
14 |
Au |
ГЦК |
196.9 |
4.08 |
19.28 |
2.2 |
165 |
6.39 |
1337 |
4.58 |
№ ВАР. |
Тип примеси |
Полупроводник |
Ширина запрещённой области |
Эффективная масса |
Подвижность при 300К |
Работа выхода, Эв |
||
EG (300 К), Эв |
m"n/me |
m’’p/me |
μn, см2·В1·с1 |
μp, см2·В1·с1 |
||||
6 |
n |
InSb |
0.17 |
0.0133 |
0.6 |
76000 |
5000 |
4.75 |
№ вар. |
3 |
концентрация примесей, м-3 |
1022 |
 Рис. 1 Изображение осей симметрии кубической решётки
Рис. 1 Изображение осей симметрии кубической решётки
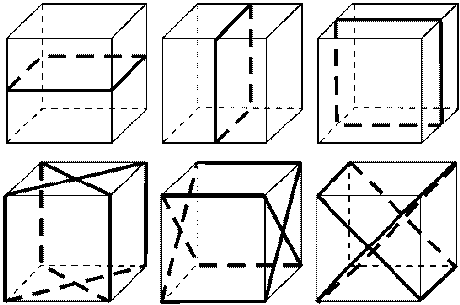 Рис. 2 Изображение плоскостей симметрии куба
Рис. 2 Изображение плоскостей симметрии куба
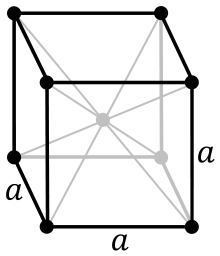 Рис. 3 Изображение центра симметрии куба
Рис. 3 Изображение центра симметрии куба
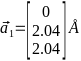 ,
, 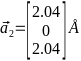 ,
, 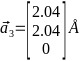 Кристаллическая решётка по заданным векторам построена на рис. 4
Кристаллическая решётка по заданным векторам построена на рис. 4
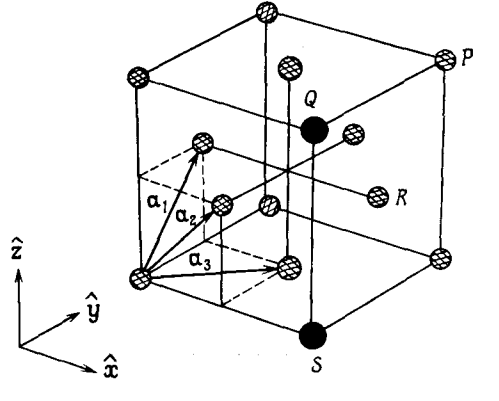 Рис. 4 Тройка основных векторов для ГЦК решётки
Рис. 4 Тройка основных векторов для ГЦК решётки
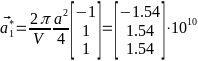 ,
, 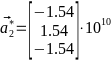 ,
, 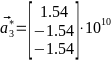 Что соответствует ОЦК. Её изображение на рис. 5.
Что соответствует ОЦК. Её изображение на рис. 5.
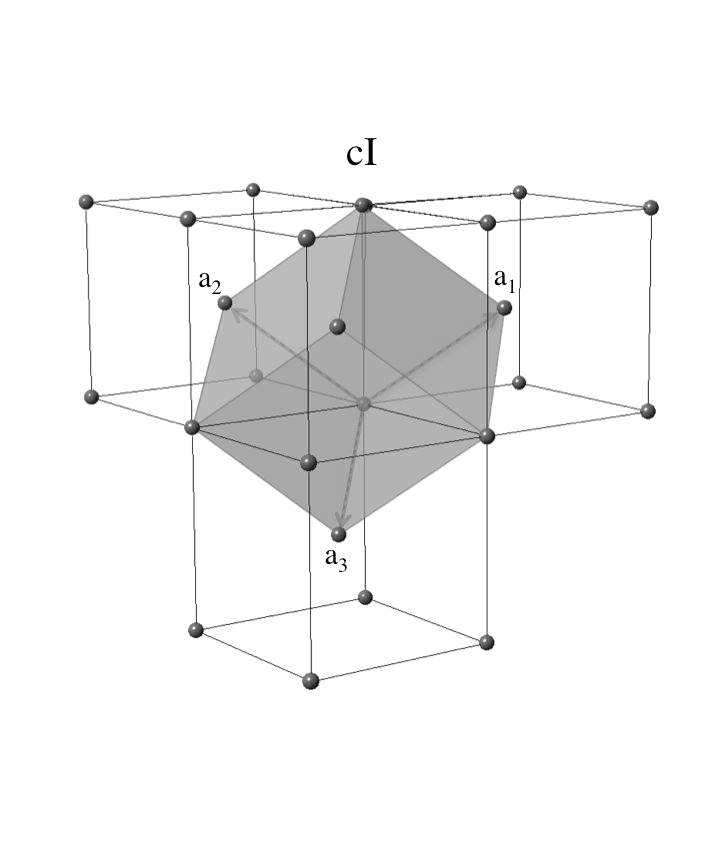 Рис. 5 Обратная решётка для ГЦК — ОЦК
Рис. 5 Обратная решётка для ГЦК — ОЦК
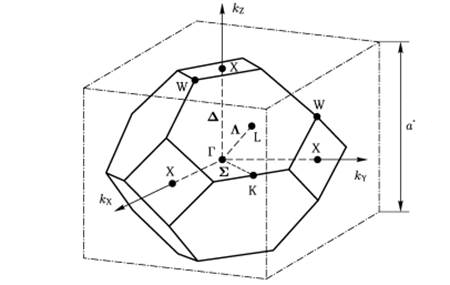 Рис. 6 Первая зона Бриллюэна
Рис. 6 Первая зона Бриллюэна
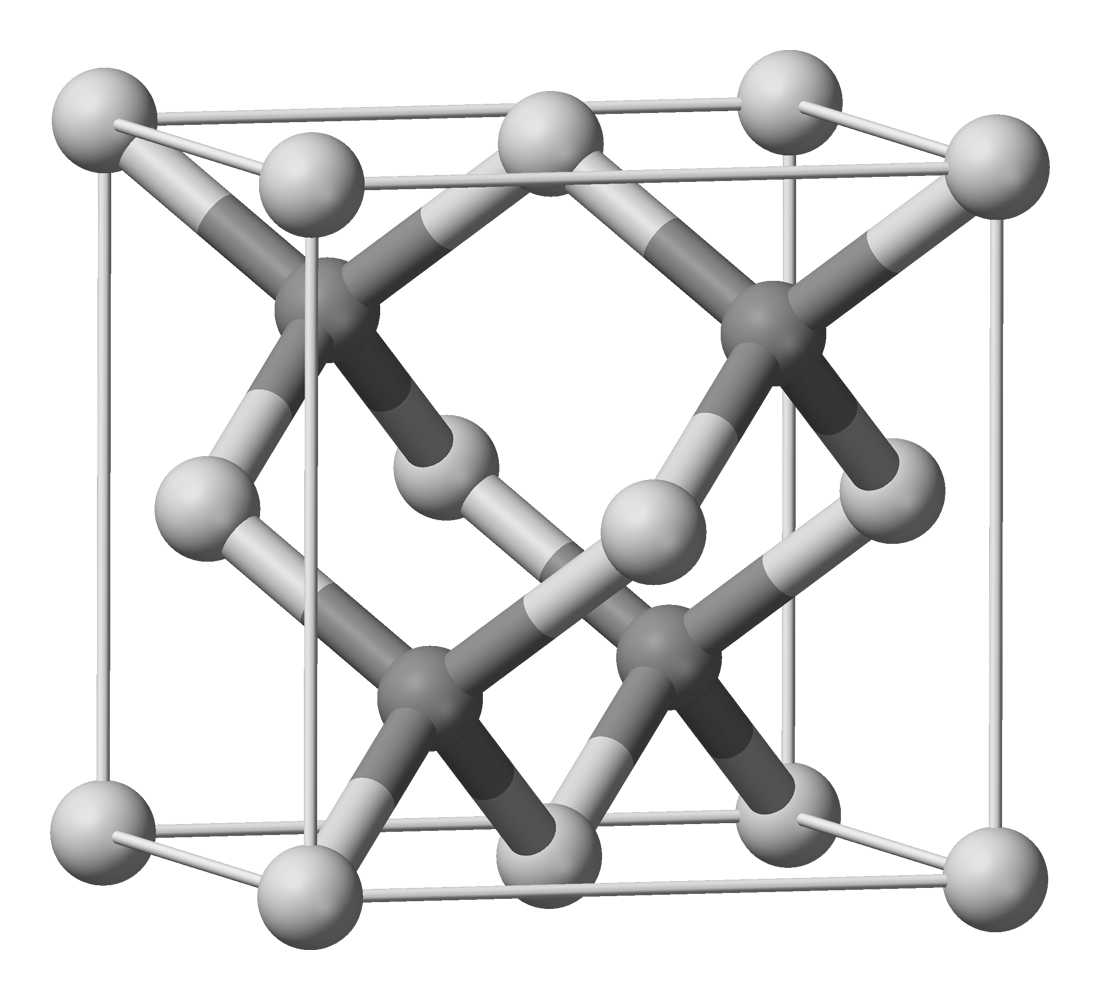 Рис. 7 Антимонид индия
Рис. 7 Антимонид индия
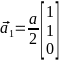 ,
, 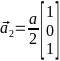 ,
, 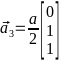 , считая, что постоянная решётки
= 1
Для параметра решётки
, считая, что постоянная решётки
= 1
Для параметра решётки 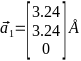 ,
, 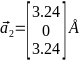 ,
, 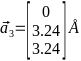 Кристаллическая решётка по заданным векторам изображена на рис. 4.
Объём элементарной ячейки аналогично предыдущему пункту:
Кристаллическая решётка по заданным векторам изображена на рис. 4.
Объём элементарной ячейки аналогично предыдущему пункту:
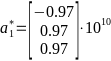 ,
, 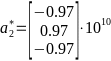 ,
, 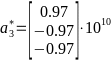 # 2) Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов.
Связь радиуса Ферми с концентрацией электронов можно выяснить из
следующего выражения:
# 2) Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов.
Связь радиуса Ферми с концентрацией электронов можно выяснить из
следующего выражения:  Рис. 8 Атомы элементарной ячейки ГЦК решётки
Рис. 8 Атомы элементарной ячейки ГЦК решётки
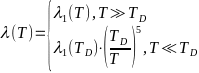 .
Где
.
Где 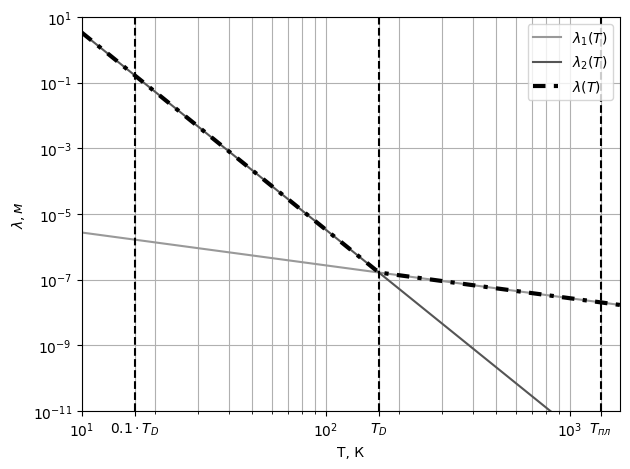 Рис. 9 График зависимости длин свободного пробега от температуры
Рис. 9 График зависимости длин свободного пробега от температуры
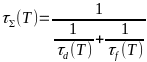 .
Оно справедливо если
один
из
механизмов рассеяния
преобладает
над другим
при
*T *=
273 *К*.
.
Оно справедливо если
один
из
механизмов рассеяния
преобладает
над другим
при
*T *=
273 *К*.
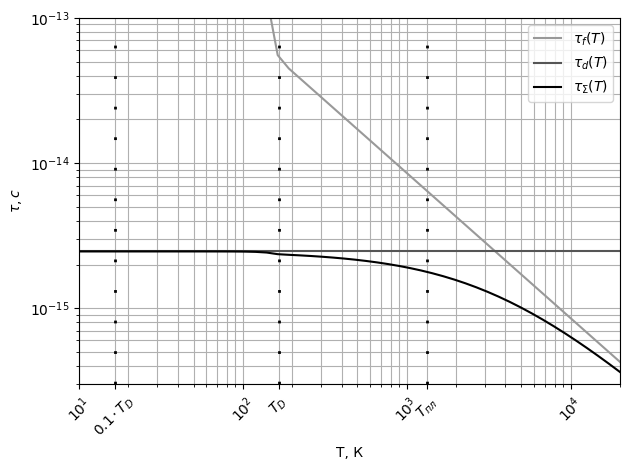 Рис. 10 График зависимости времени релаксации
от
температуры
Рис. 10 График зависимости времени релаксации
от
температуры
|
|
TD |
Tпл |
10-12 |
10-12 |
|
|
10-13 |
10-13 |
|
|
10-14 |
10-14 |
|
|
|
|
TD |
Tпл |
10-12 |
|
|
|
10-13 |
|
|
|
10-14 |
|
|
|
|
|
TD |
Tпл |
10-12 |
|
|
|
10-13 |
805 |
|
|
10-14 |
80.5 |
675 |
|
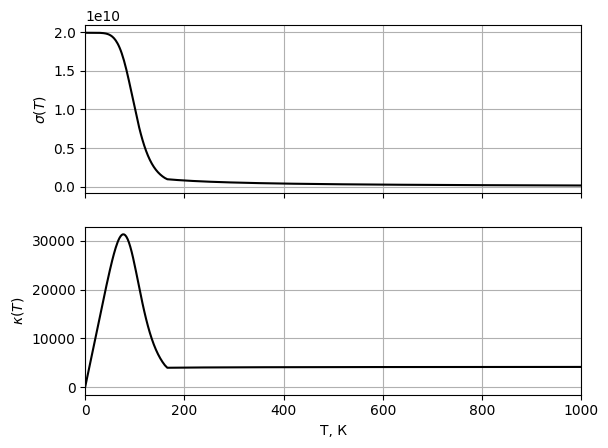 Рис. 11
Графики
зависимости электропроводности и
теплопроводности при
Рис. 11
Графики
зависимости электропроводности и
теплопроводности при 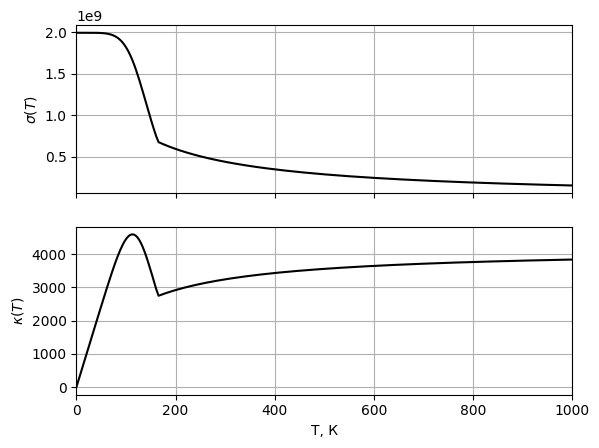 Рис. 12 Графики
зависимости электропроводности и
теплопроводности при
Рис. 12 Графики
зависимости электропроводности и
теплопроводности при 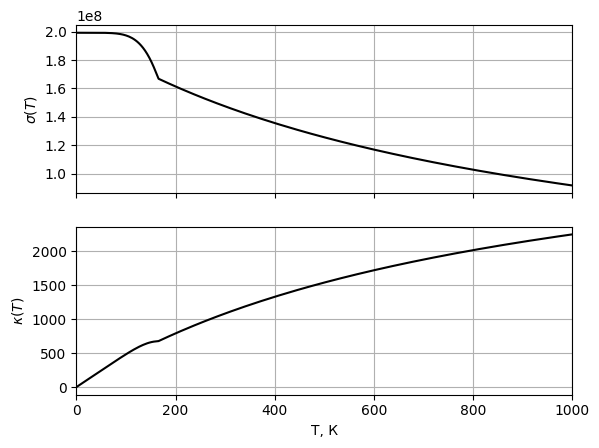 Рис. 13 Графики
зависимости электропроводности и
теплопроводности при
Рис. 13 Графики
зависимости электропроводности и
теплопроводности при 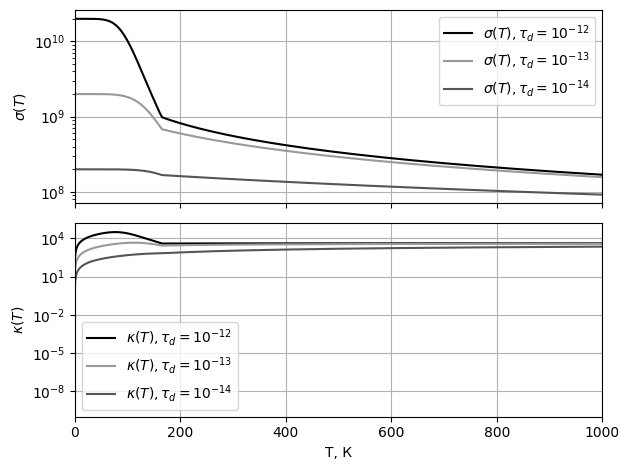 Рис. 14 Графики электропроводностей и теплопроводностей
при различных
Рис. 14 Графики электропроводностей и теплопроводностей
при различных 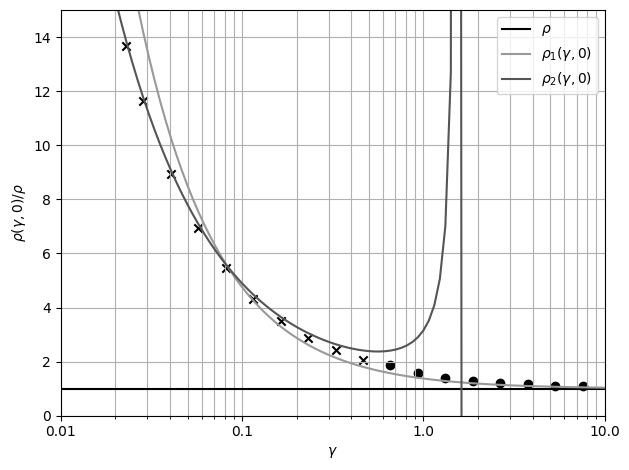 Рис. 15 График удельного сопротивления от толщины плёнки при параметре
зеркальности 0
Рис. 15 График удельного сопротивления от толщины плёнки при параметре
зеркальности 0
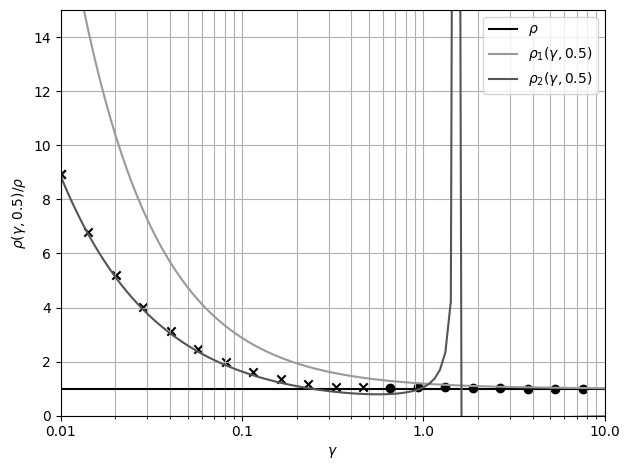 Рис. 16 График удельного сопротивления от толщины плёнки при параметре
зеркальности 0.5
Рис. 16 График удельного сопротивления от толщины плёнки при параметре
зеркальности 0.5
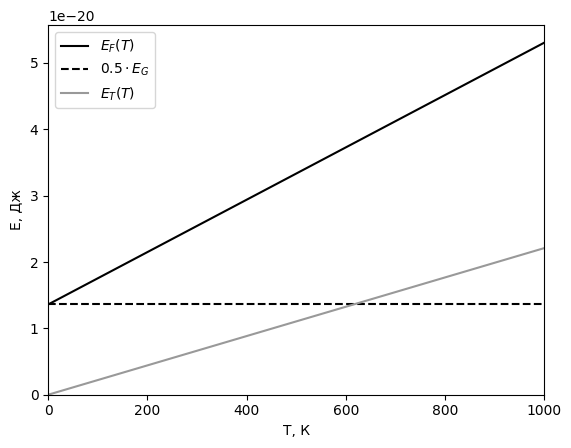 Рис. 17 График температурной зависимости энергии Ферми и тепловой
энергии
Рис. 17 График температурной зависимости энергии Ферми и тепловой
энергии
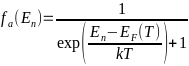 . Например, для
. Например, для 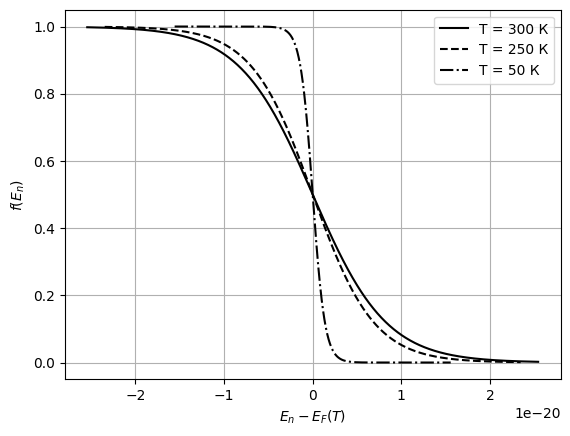 Рис. 18 Распределение Ферми-Дирака носителей заряда по энергиям при
Рис. 18 Распределение Ферми-Дирака носителей заряда по энергиям при 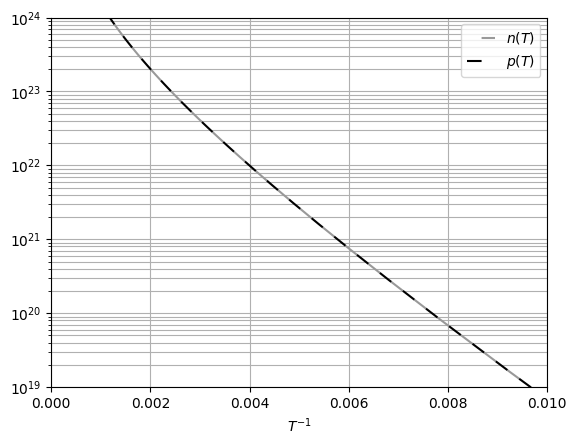 Рис. 19 График зависимостей концентрации электронов и дырок от
температуры
Рис. 19 График зависимостей концентрации электронов и дырок от
температуры
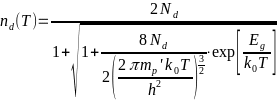 Кроме этого, справедливы аппроксимации:
Кроме этого, справедливы аппроксимации:
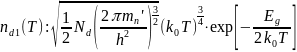
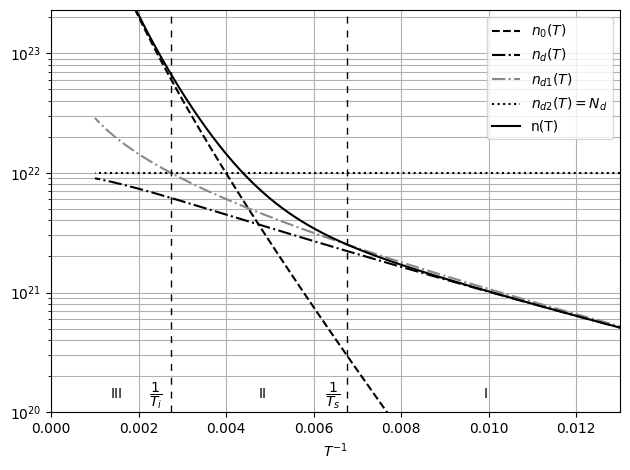 Рис. 20 График зависимости концентрации зарядов в примесном проводнике
от обратной температуры
Рис. 20 График зависимости концентрации зарядов в примесном проводнике
от обратной температуры
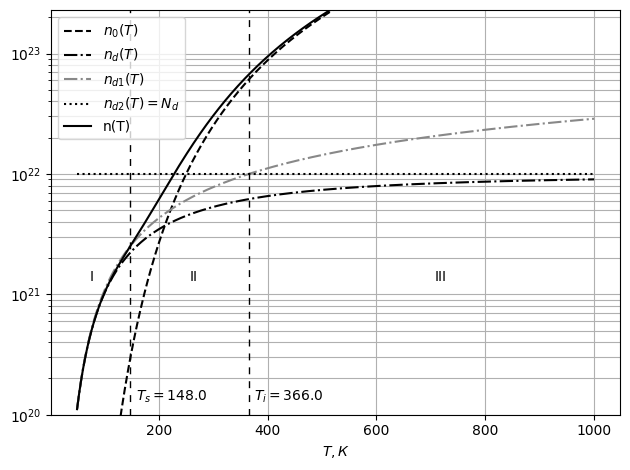 Рис. 21 График зависимости концентрации зарядов в примесном проводнике
от температуры
Рис. 21 График зависимости концентрации зарядов в примесном проводнике
от температуры
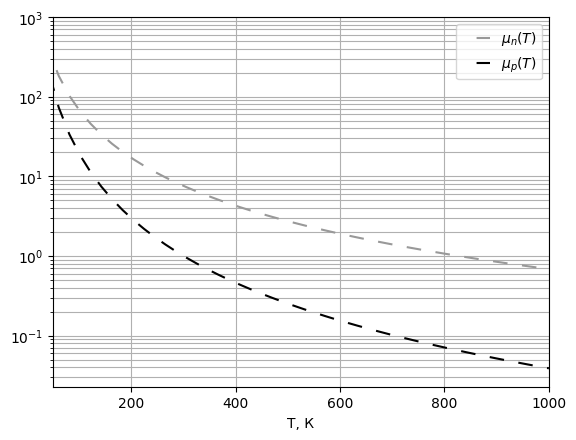 Рис. 22 График подвижностей электронов и дырок
Рис. 22 График подвижностей электронов и дырок
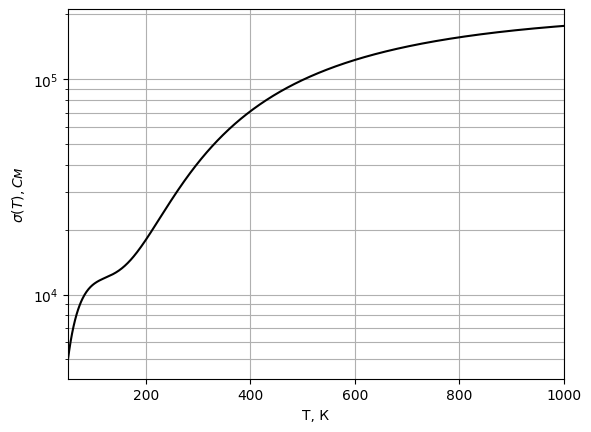 Рис. 23 График электропроводности примесного полупроводника
Рис. 23 График электропроводности примесного полупроводника
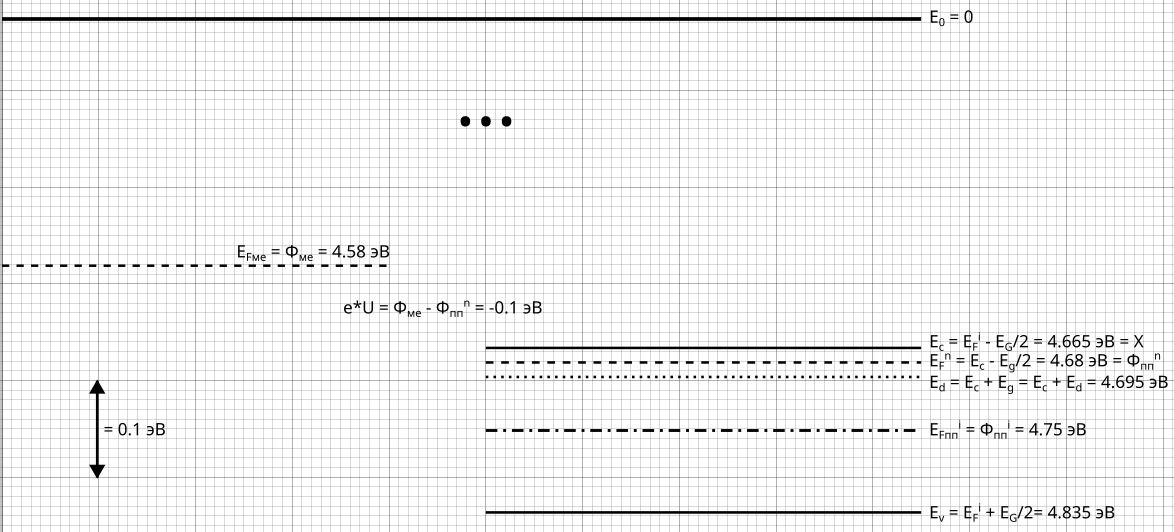 Рис. 24 Энергетическая диаграмма металл-вакуум-полупроводник
Рис. 24 Энергетическая диаграмма металл-вакуум-полупроводник
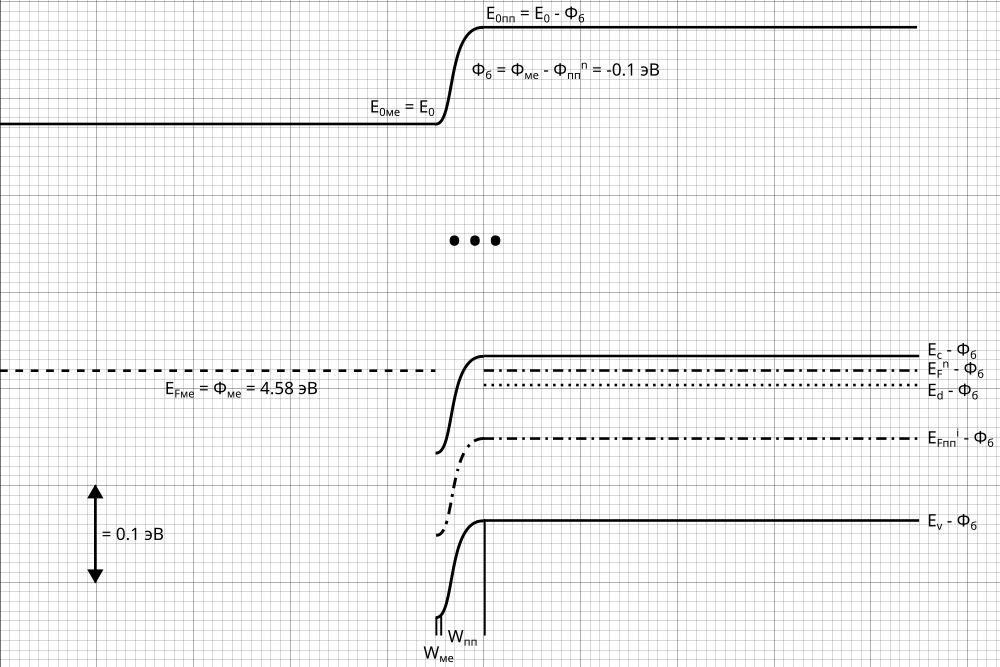 Рис. 25 Энергетическая диаграмма металл-полупроводник
Рис. 25 Энергетическая диаграмма металл-полупроводник
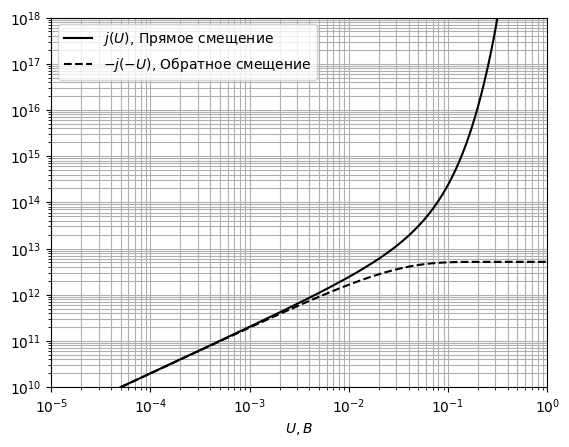 Рис. 28 ВАХ контакта при *T* = 300 *К*
Рис. 28 ВАХ контакта при *T* = 300 *К*
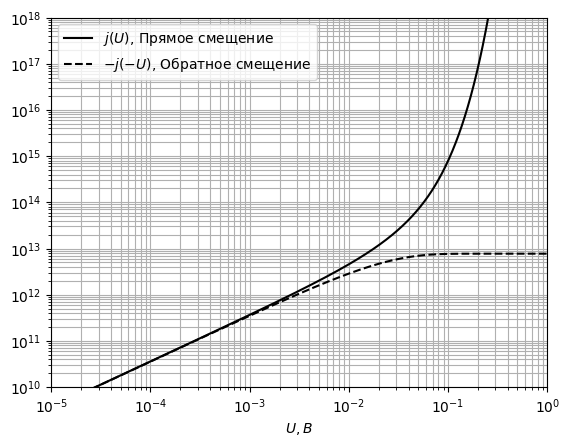 Рис. 29 ВАХ контакта при *T* = 250 *К*
Рис. 29 ВАХ контакта при *T* = 250 *К*
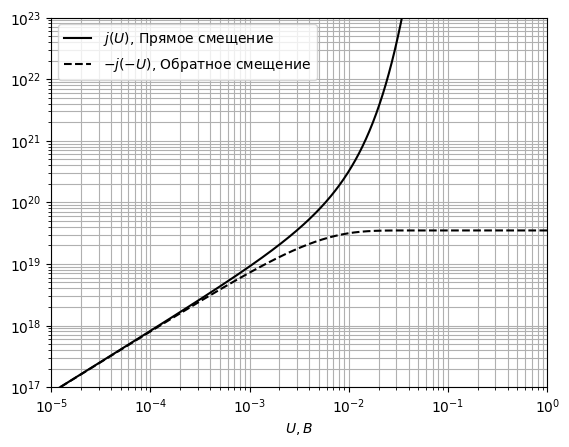 Рис. 30 ВАХ контакта при *T* = 50 *К*
Рис. 30 ВАХ контакта при *T* = 50 *К*