diff --git a/README.html b/README.html
deleted file mode 100644
index 415d425..0000000
--- a/README.html
+++ /dev/null
@@ -1,1984 +0,0 @@
-
-
-
-
-
-
-
-
-
-
-
-МИНОБРНАУКИ
-РОССИИ
-
-Санкт-Петербургский
-государственный
-
-электротехнический
-университет
-
-«ЛЭТИ»
-им. В.И. Ульянова (Ленина)
-
-Кафедра
-Микрорадиоэлектроники и технологии
-радиоаппаратуры
-
-
-(МИТ)
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-ОТЧЕТ
-
-по
-ИДЗ
-
-по
-дисциплине «ОЭиР»
-
-Тема:
-Исследование контактных явлений в
-структуре металл-полупроводник
-
-
-
-
-
-Вариант
-25
-14,6,3
-
-https://www.meme-arsenal.com/memes/4598e00877a721c55a46dc4aafb78719.jpg
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- Студент
- гр. 1181
- |
-
-
-
-
- |
-
- Шишков
- Д.А.
- |
-
-
-
- Преподаватель
- |
-
-
-
-
- |
-
- Ситникова
- М.Ф.
- |
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-Санкт-Петербург
-
-2023
-
-
-
-
-
-
-Задание
-
-Для
-заданной пары металл-полупроводник
-оценить кинетические свойства заданных
-материалов, рассчитать и построить
-энергетическую диаграмму и вольт-амперную
-характеристику контакта в заданном
-диапазоне температур, дать рекомендации
-по применению исследуемого контакта.
-
-Таблица
-1. Некоторые свойства металлов
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- No
- ВАР.
- |
-
- Элемент
- |
-
- Структура
- |
-
- Атомная
- масса
- |
-
- Параметр
- решетки, Å
- |
-
- Плотность,
- г/см3
- |
-
- Удельное
- сопротивление, мкОм·см
- |
-
- Температура,
- К
- |
-
- Работа
- выхода φ, эВ
- |
-
-
-
- Дебая
- (TD)
- |
-
- Ферми
- (TF·10-4)
- |
-
- плавления
- (Tпл)
- |
-
-
-
- 14
- |
-
- Au
- |
-
- ГЦК
- |
-
- 196.9
- |
-
- 4.08
- |
-
- 19.28
- |
-
- 2.2
- |
-
- 165
- |
-
- 6.39
- |
-
- 1337
- |
-
- 4.58
- |
-
-
-
-
-
-
-
-Таблица
-2. Свойства cобственных полупроводников
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- № ВАР.
- |
-
- Тип
- примеси
- |
-
- Полупроводник
- |
-
- Ширина
- запрещённой области
- |
-
- Эффективная
- масса
- |
-
- Подвижность
- при 300К
- |
-
- Работа
- выхода, Эв
- |
-
-
-
- EG
- (300 К), Эв
- |
-
- m"n/me
- |
-
- m’’p/me
- |
-
- μn,
- см2·В1·с1
- |
-
- μp,
- см2·В1·с1
- |
-
-
-
- 6
- |
-
- n
- |
-
- InSb
- |
-
- 0.17
- |
-
- 0.0133
- |
-
- 0.6
- |
-
- 76000
- |
-
- 5000
- |
-
- 4.75
- |
-
-
-
-
-
-
-
-Таблица
-3. Концентрация n- и p- примесей в
-полупроводниках
-
-
-
-
-
-
-
- № вар.
- |
-
- 3
- |
-
-
-
- концентрация
- примесей, м-3
- |
-
- 1022
- |
-
-
-
-
-
-
-
-
-
-
-
-1) Определить класс симметрии заданных
-материалов, построить прямую и обратную
-элементарные ячейки заданных материалов.
-Определить размеры Зоны Бриллюэна в
-направлениях X, L, К.
-
-1.1) Металл — золото (Au):
-
-Структура:
-Гранецентрированная кубическая решётка
-
-Формула
-симметрии: 3L44L36L29PC
-
-Класс
-симметрии: m3m
-
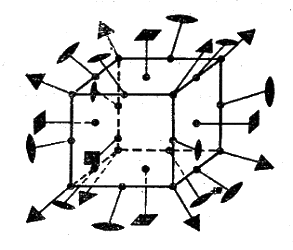
-Так
-как формулы симметрии ГЦК и простой
-кубической решётки совпадают, на рис.
-1-3 приведены изображения осей, плоскостей
-и центра симметрии для последнего
-
- -
-
-
-Рис.
-1 Изображение осей симметрии кубической
-решётки
-
-
-
-
-
- -
-
-
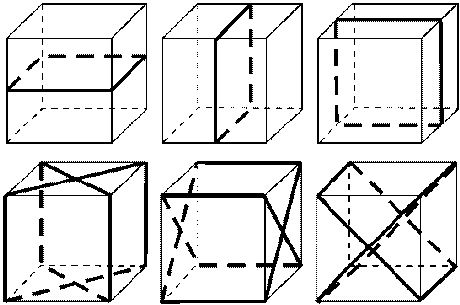
-Рис.
-2 Изображение плоскостей симметрии куба
-
- -
-
-
-Рис.
-3 Изображение центра симметрии куба
-
-Базисные
-вектора:
-
-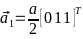 -,
-
-,
-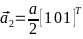 -,
-
-,
-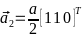 -
-
-
-Подставляя
-параметр решётки
-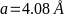 -
-
-
-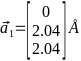 -,
-
-,
-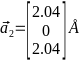 -,
-
-,
-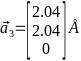 -
-
-
-Кристаллическая
-решётка по заданным векторам построена
-на рис. 4
-
-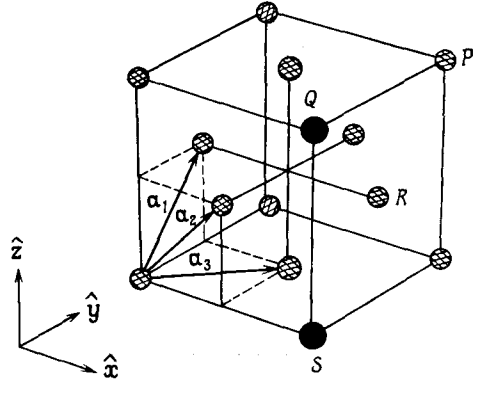 -
-
-
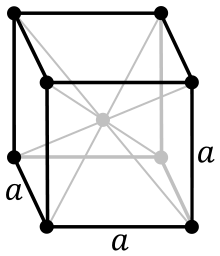
-Рис.
-4 Тройка основных векторов для ГЦК
-решётки
-
-Объём
-элементарной ячейки:
-
-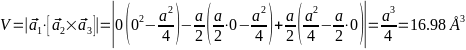 -
-
-
-Базисные
-вектора обратной решётки:
-
-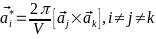 -;
-
-;
-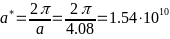 -
-
-
-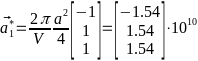 -,
-
-,
-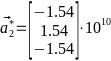 -,
-
-,
-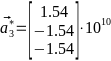 -
-
-
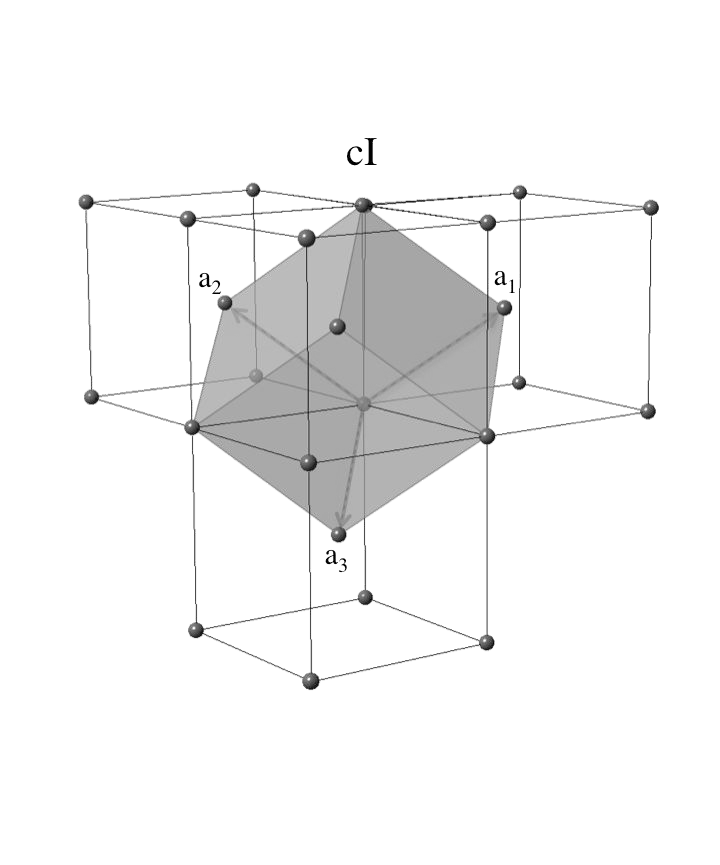
-Что
-соответствует ОЦК. Её изображение на
-рис. 5.
-
- -
-
-
-Рис.
-5 Обратная решётка для ГЦК — ОЦК
-
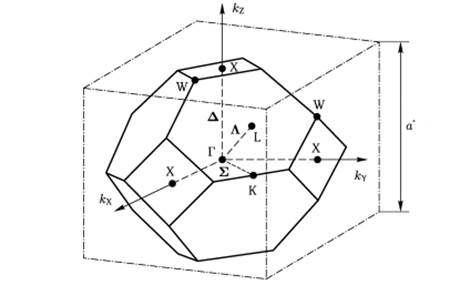
-Первая
-зона Бриллюэна (рис. 6):
-
- -
-
-
-Рис.
-6 Первая зона Бриллюэна
-
-Размеры
-зоны Бриллюэна по направлениям X, L, K:
-
-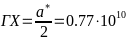 -
--
-центр верхнего квадрата, по направлению
-[001]
-
--
-центр верхнего квадрата, по направлению
-[001]
-
-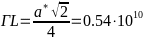 -
--
-центр шестиугольника, по направлению
-[111]
-
--
-центр шестиугольника, по направлению
-[111]
-
-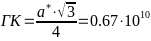 -
--
-середина грани соединяющей два
-шестиугольника, по направлению [101]
-
--
-середина грани соединяющей два
-шестиугольника, по направлению [101]
-
-1.2) Полупроводник - антимонид индия
-(InSb)
-
-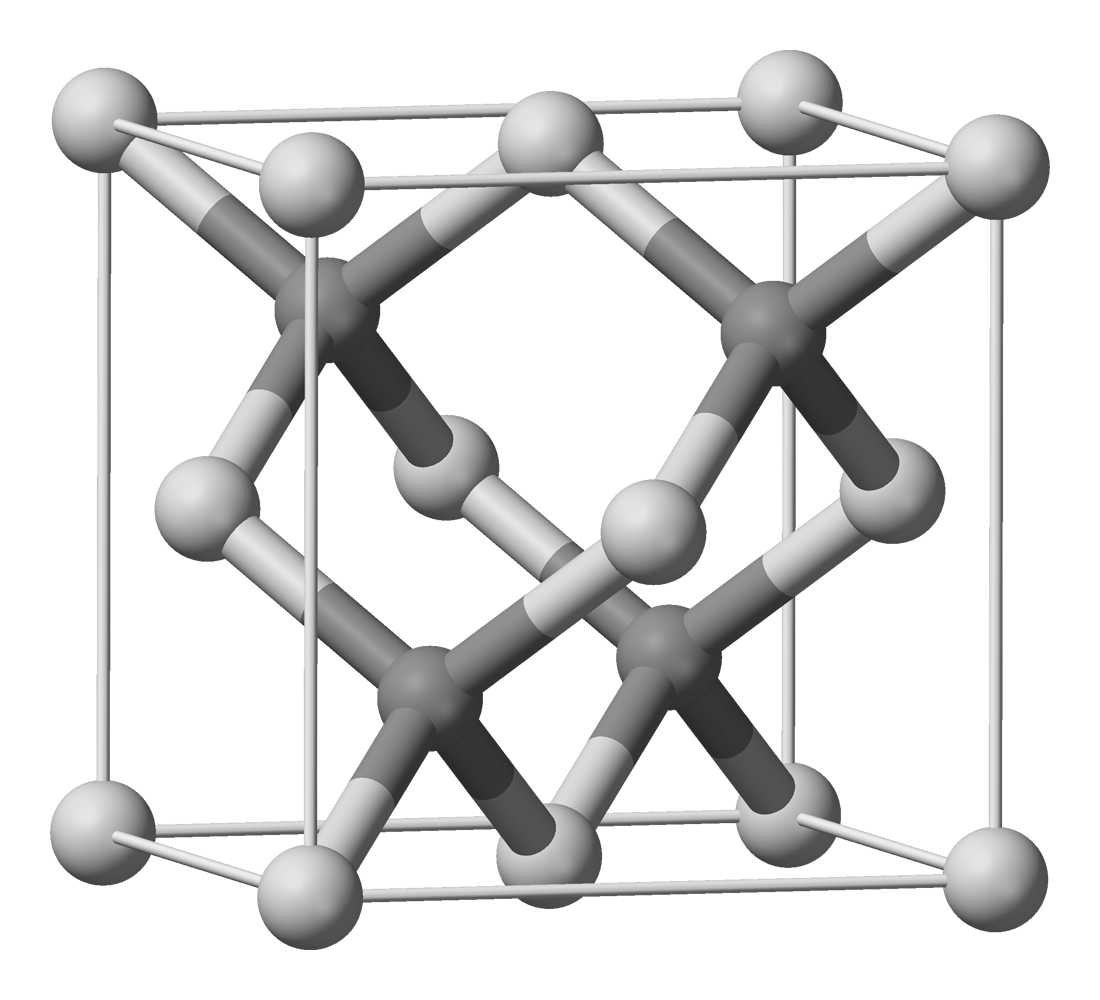 -
-
-
-Рис.
-7 Антимонид индия
-
-Структура:
-Гранецентрированная кубическая решётка
-
-Формула
-симметрии: 3L44L36L29PC
-
-Класс
-симметрии: m3m
-
-Изображения
-осей, плоскостей и центра симметрии для
-последнего — см. рис. 1-3.
-
-Базисные
-вектора:
-
-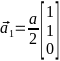 -,
-
-,
-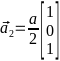 -,
-
-,
-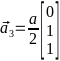 -,
-считая, что постоянная решётки = 1
-,
-считая, что постоянная решётки = 1
-
-Для
-параметра решётки
-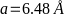 -
-
-
-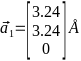 -,
-
-,
-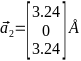 -,
-
-,
-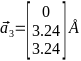 -
-
-
-Кристаллическая
-решётка по заданным векторам изображена
-на рис. 4.
-
-Объём
-элементарной ячейки аналогично
-предыдущему пункту:
-
-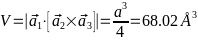 -
-
-
-Базисные
-вектора в обратном пространстве:
-
-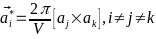 -;
-
-;
-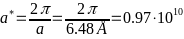 -
-
-
-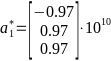 -,
-
-,
-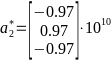 -,
-
-,
-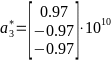 -
-
-
-
-
-
-
-2) Определить концентрацию электронов
-для заданного металла из условия касания
-зоны Бриллюэна и сферы Ферми и сделать
-суждение о применимости теории свободных
-электронов.
-
-Связь
-радиуса Ферми с концентрацией электронов
-можно выяснить из следующего выражения:
-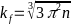 -.
-С другой стороны
-введено условие
-касания сферы Ферми с границей зоны
-Бриллюэна. Из п. 1 известно, что наименьшие
-размеры она имеет по направлению
-
-.
-С другой стороны
-введено условие
-касания сферы Ферми с границей зоны
-Бриллюэна. Из п. 1 известно, что наименьшие
-размеры она имеет по направлению
-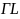 -,
-следовательно радиус
-Ферми для вписанной сферы
-
-,
-следовательно радиус
-Ферми для вписанной сферы
-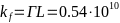 -
-
-
-Тогда
-концентрация электронов:
-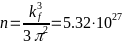 -
-
-
-Концентрацию
-свободных электронов в металле также
-можно определить пользуясь приближением
-слабой связи для:
-
-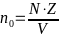 -,
-где Z — его валентность, N — количество
-атомов в его элементарной ячейке, а V —
-её объём.
-,
-где Z — его валентность, N — количество
-атомов в его элементарной ячейке, а V —
-её объём.
-
-Для
-золота:
-
-В
-элементарной ГЦК решётке N = 4 атома (см.
-рис. 8)
-
- -
-
-
-Рис.
-8 Атомы элементарной ячейки ГЦК решётки
-
-При
-Z = 1
-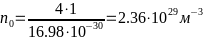 -
-
-
-При
-Z = 2
-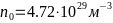 -
-
-
-При
-Z = 3
-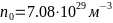 -
-- наиболее частая
-
-- наиболее частая
-
-Вывод:
-Как видно,
-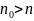 -
-для любой возможной валентности,
-следовательно, теория свободных
-электронов не применима. Тогда эффективную
-массу электрона примем равной массе
-свободного электрона
-
-
-для любой возможной валентности,
-следовательно, теория свободных
-электронов не применима. Тогда эффективную
-массу электрона примем равной массе
-свободного электрона
-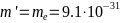 -
-кг. В сравнении со стандартным металлом
-Пиппарда, у которого плотность электронов
-
-
-кг. В сравнении со стандартным металлом
-Пиппарда, у которого плотность электронов
-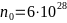 -,
-а радиус Ферми
-
-,
-а радиус Ферми
-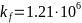 -,
-у золота они получаются большими
-
-,
-у золота они получаются большими
-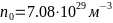 -,
-
-,
-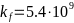 -.
-.
-
-
-
-
-3) Рассчитать и построить зависимости
-средней длины свободного пробега,
-времени релаксации и электропроводности
-от температуры для металла в диапазоне
-температур (0,1 - 10) ТD. Оценить
-степень дефектности металла по заданной
-величине удельного сопротивления.
-
-3.1) Исследование температурной зависимости
-длины свободного пробега
-
-Длина
-свободного пробега электронов в
-зависимости от температуры (если она
-много больше температуры Дебая, то
-происходит упругое рассеяние, иначе -
-неупругое) приблизительно рассчитывается
-согласно следующему выражению:
-
-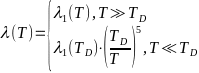 -.
-.
-
-Где
-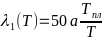 -,
-
-,
-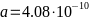 -
-— параметр решётки,
-
-
-— параметр решётки,
-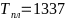 -
-— температура плавления
-
-
-— температура плавления
-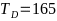 -
-— температура Дебая.
-
-— температура Дебая.
-
-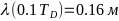 -,
-
-,
-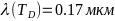 -,
-
-,
-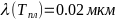 -
-
-
-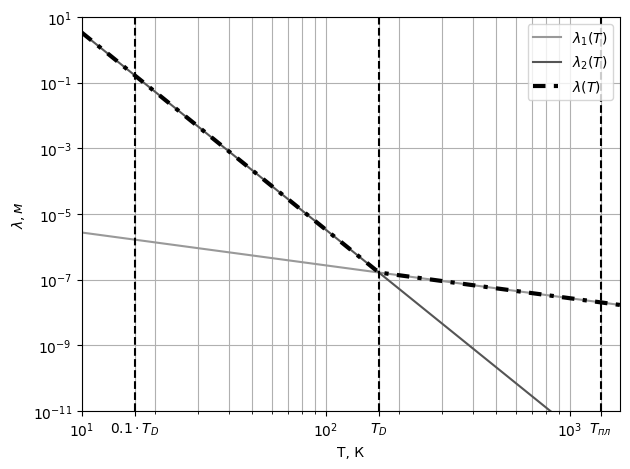 -
-
-
-Рис.
-9 График зависимости длин свободного
-пробега от температуры
-
-Вывод:
-с ростом температуры длина свободного
-пробега действительно уменьшается.
-
-3.2) Исследование влияния дефектов на
-время релаксации
-
-Время
-релаксации для рассеивания на дефектах:
-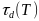 -
-
-
-Время
-релаксации для электрон-фононного
-рассеивания
-в
-зависимости от температуры:
-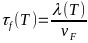 -,
-где
-
-,
-где
-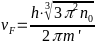 -
-—
-скорость
-электронов на поверхности Ферми. В
-последней формуле
-
-
-—
-скорость
-электронов на поверхности Ферми. В
-последней формуле
-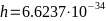 -
-— постоянная
-Планка,
-
-
-— постоянная
-Планка,
-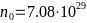 -
-— концентрация носителей
-заряда,
-
-
-— концентрация носителей
-заряда,
-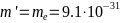 -
-—
-эффективная масса электрона.
-
-—
-эффективная масса электрона.
-
-Тогда,
-согласно правилу
-Маттиссена
-суммарное
-время релаксации получается следующим:
-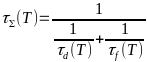 -.
-.
-
-Оно
-справедливо если один
-из
-механизмов рассеяния
-преобладает
-над
-другим при
-T
-=
-273
-К.
-
-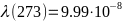 -;
-
-;
-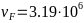 -;
-
-;
-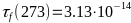 -
-
-
-Воспользуемся
-формулой
-для электропроводности:
-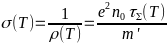 -,
-где
-
-,
-где
- -
-— заряд электрона,
-
-
-— заряд электрона,
-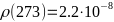 -
-— удельное
-сопротивление золота при Н.У.
-
-
-— удельное
-сопротивление золота при Н.У.
-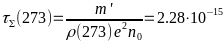 -.
-.
-
-Подставив
-эти
-значения
-в правило
-Маттиссена,
-получим
-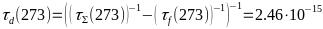 -.
-.
-
-Вывод:
-преобладает механизм
-рассеивания на дефектах,
-так
-как его время релаксации меньше.
-В
-сравнении со
-стандартным металлом Пиппарда, у
-которого скорость электронов на
-поверхности Ферми
-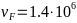 -,
-у
-золота она
-выше:
-
-
-,
-у
-золота она
-выше:
-
-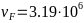 -.
-.
-
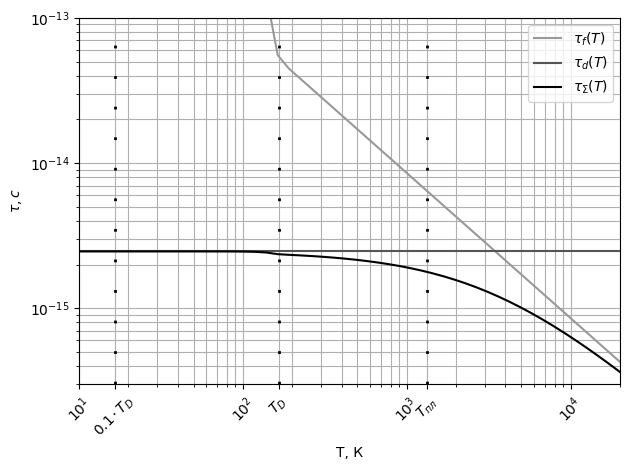
-Построим
-график
-зависимости времени
-релаксации
-от
-температуры
-для
-обоих
-механизмов рассеивания и суммарный,
-считая что
-на дефектах оно
-будет
-постоянным.
-
- -
-
-
-Рис.
-10 График зависимости
-времени
-релаксации от
-температуры
-
-Для
-разных
-температур и времён
-релаксации для
-рассеяния
-на
-дефектах
-вычислим
-общее
-время релаксации по
-правилу
-Маттиссена:
-
-
-
-Таблица
-4. Суммарное время релаксации
-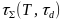 -
-
-
-
-
-
-
-
-
-
-
-
-
- 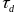 -\T
-\T
- |
-
- 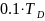 -
-
- |
-
- TD
- |
-
- Tпл
- |
-
-
-
- 10-12
- |
-
- 10-12
- |
-
- 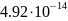 -
-
- |
-
- 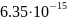 -
-
- |
-
-
-
- 10-13
- |
-
- 10-13
- |
-
- 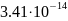 -
-
- |
-
- 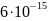 -
-
- |
-
-
-
- 10-14
- |
-
- 10-14
- |
-
-  -
-
- |
-
- 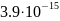 -
-
- |
-
-
-
-
-
-
-
-Вывод:
-С ростом температуры
-суммарное
-время релаксации
-уменьшается.
-
-3.3) Исследование температурной зависимости
-электропроводности и теплопроводности
-металлов
-
-Теплопроводность
-металла можно определить исходя
-из закона Видемана-Франца:
-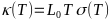 -,
-где
-
-,
-где
-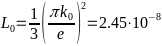 -
-—
-число
-Лоренца, в
-чьей формуле присутствует
-
-
-—
-число
-Лоренца, в
-чьей формуле присутствует
-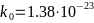 -
-— постоянная Больцмана,
-а
-
-
-— постоянная Больцмана,
-а
-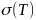 -
-— электропроводность,
-выраженная через время релаксации из
-предыдущего подпункта.
-
-— электропроводность,
-выраженная через время релаксации из
-предыдущего подпункта.
-
-Для
-разных температур и времён релаксации
-для рассеяния на дефектах вычислим
-электропроводность и теплопроводность:
-
-Таблица
-5.
-Значения
-электропроводности
-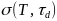 -
-
-
-
-
-
-
-
-
-
-
-
-
- 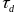 -\T
-\T
- |
-
- 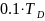 -
-
- |
-
- TD
- |
-
- Tпл
- |
-
-
-
- 10-12
- |
-
- 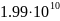 -
-
- |
-
- 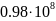 -
-
- |
-
- 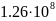 -
-
- |
-
-
-
- 10-13
- |
-
- 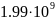 -
-
- |
-
-  -
-
- |
-
- 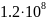 -
-
- |
-
-
-
- 10-14
- |
-
- 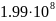 -
-
- |
-
- 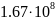 -
-
- |
-
- 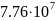 -
-
- |
-
-
-
-
-
-
-
-Таблица
-6.
-Значения
-иеплопроводности
-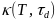 -
-
-
-
-
-
-
-
-
-
-
-
-
- 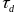 -\T
-\T
- |
-
- 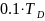 -
-
- |
-
- TD
- |
-
- Tпл
- |
-
-
-
- 10-12
- |
-
- 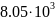 -
-
- |
-
- 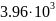 -
-
- |
-
- 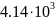 -
-
- |
-
-
-
- 10-13
- |
-
- 805
- |
-
- 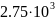 -
-
- |
-
- 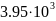 -
-
- |
-
-
-
- 10-14
- |
-
- 80.5
- |
-
- 675
- |
-
- 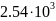 -
-
- |
-
-
-
-
-
-
-
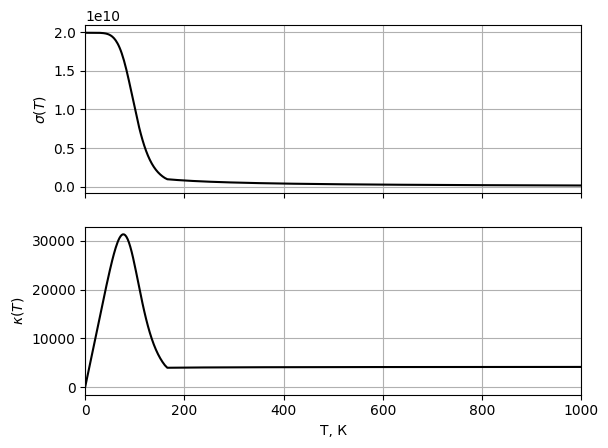
-Изобразим
-их на графиках:
-
- -
-
-
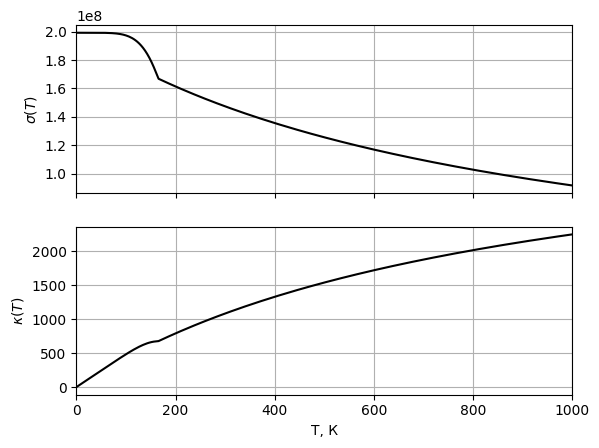
-Рис.
-11
-Графики
-зависимости электропроводности
-и теплопроводности
-при
-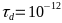 -
-
-
-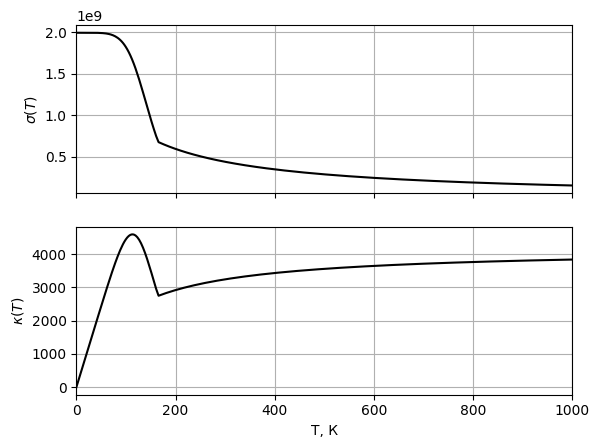 -
-
-
-Рис.
-12 Графики
-зависимости электропроводности
-и теплопроводности
-при
-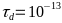 -
-
-
- -
-
-
-Рис.
-13 Графики
-зависимости электропроводности
-и теплопроводности
-при
-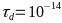 -
-
-
-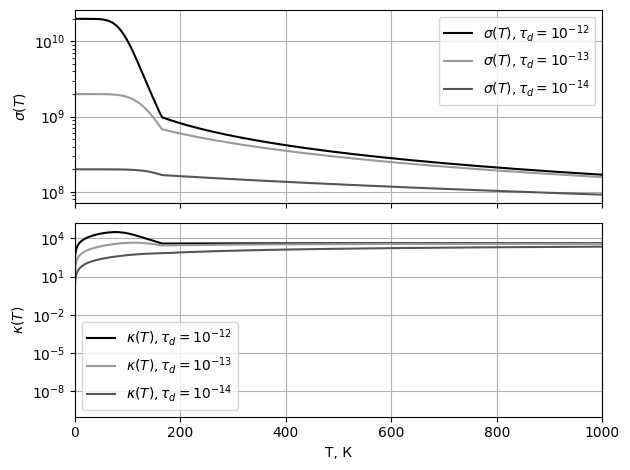 -
-
-
-Рис.
-14 Графики электропроводностей
-и теплопроводностей при
-различных
-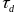 -
-
-
-Вывод:
-С ростом концентрации
-дефектов (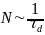 -)
-температурные
-зависимости электропроводности
-и теплопроводности
-«выпрямляются»,
-вместе с чем также
-уменьшается их
-значение в каждой точке.
-При этом, с
-ростом температуры
-электропроводность
-убывает, а теплопроводность
-возрастает.
-)
-температурные
-зависимости электропроводности
-и теплопроводности
-«выпрямляются»,
-вместе с чем также
-уменьшается их
-значение в каждой точке.
-При этом, с
-ростом температуры
-электропроводность
-убывает, а теплопроводность
-возрастает.
-
-3.4) Оценить степень дефектности металла
-по заданной величине удельного
-сопротивления
-
-Как
-было вычислено в подпункте 3.2, время
-релаксации для рассеивания на дефектах
- -.
-Тогда количество дефектов в металле
-
-.
-Тогда количество дефектов в металле
-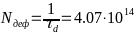 -.
-
-
-.
-
-
-
-Вывод:
-В сравнении с
-концентрацией
-носителей
-заряда
-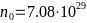 -,
-количество
-дефектов
-меньше
-на
-10
-порядков, что можно
-назвать приемлемым значением.
-,
-количество
-дефектов
-меньше
-на
-10
-порядков, что можно
-назвать приемлемым значением.
-
-
-
-
-
-4)
-Рассчитать и построить зависимость
-электропроводности от толщины
-металлической пленки
-при заданной температуре. Определить
-минимально возможную толщину металлизации.
-
-Графики
-зависимости электропроводности плёнки
-от толщины
-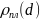 -
-будут построены для двух значений
-параметра зеркальности p1 = 0
-и p2 = 0.5 в диапазоне температур
-
-
-будут построены для двух значений
-параметра зеркальности p1 = 0
-и p2 = 0.5 в диапазоне температур
-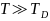 -.
-.
-
-В
-предыдущем пункте при T = Tпл
-— температуре плавления была рассчитана
-длина свободного пробега
-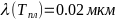 -.
-Удельное сопротивление объёмного
-образца
-
-.
-Удельное сопротивление объёмного
-образца
-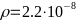 -.
-.
-
-Для
-«толстой плёнки» при параметре
-зеркальности p < 1 справедлива
-следующая формула:
-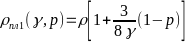 -.
-Аналогично, для «тонкой плёнки»
-
-.
-Аналогично, для «тонкой плёнки»
-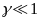 -:
-
-:
-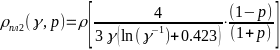 -,
-где
-
-,
-где
-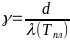 -
-
-
- -
-
-
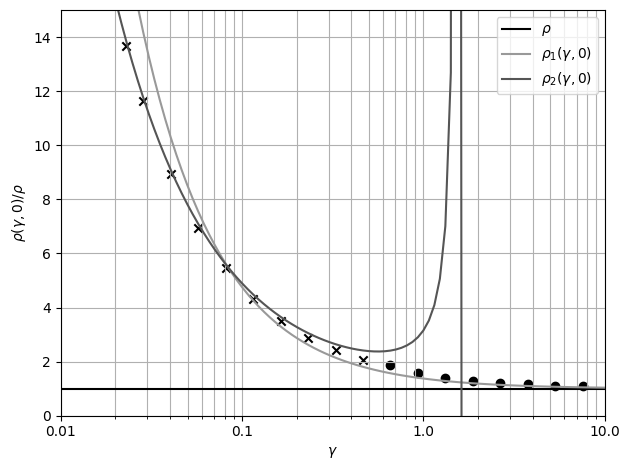
-Рис.
-15 График удельного сопротивления от
-толщины плёнки при параметре зеркальности
-0
-
- -
-
-
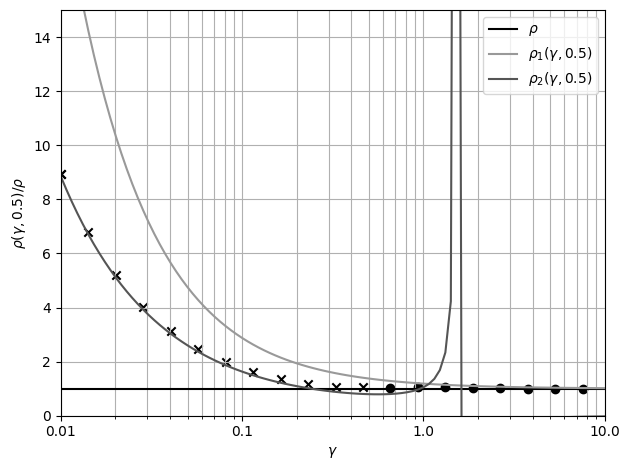
-Рис.
-16 График удельного сопротивления от
-толщины плёнки при параметре зеркальности
-0.5
-
-При
-p = 1 (весь импульс электрона по направлению
-тока сохраняется), размерный эффект
-отсутствует
-
-Минимальную
-возможную толщину металлизации можно
-определить из вышеприведённых графиков,
-выбрав такую
-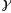 -,
-что при заданном масштабе
-
-,
-что при заданном масштабе
-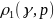 -
-практически сольётся с
-
-
-практически сольётся с
-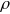 -.
-Для данного металла это будет
-
-.
-Для данного металла это будет
-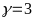 -.
-Тогда толщина
-
-.
-Тогда толщина
-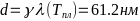 -
-
-Вывод: тонкие
-плёнки обладают низкой электропроводностью,
-однако, уже начиная с толщины
- -
-плёнка из золота должна демонстрировать
-металлические свойства. При этом, при
-большем коэффициенте зеркальности
-поверхности, действительно, удельное
-сопротивление по мере уменьшения толщины
-плёнки возрастает в меньшей степени.
-
-плёнка из золота должна демонстрировать
-металлические свойства. При этом, при
-большем коэффициенте зеркальности
-поверхности, действительно, удельное
-сопротивление по мере уменьшения толщины
-плёнки возрастает в меньшей степени.
-
-
-
-
-
-5) Определить эффективную массу носителей
-заряда, их концентрацию и степень
-вырождения электронно-дырочного газа
-в заданном собственном полупроводнике
-в данном диапазоне температур. Рассчитать
-и построить зависимости концентрации,
-подвижности и электропроводности от
-температуры для заданного примесного
-полупроводника.
-
-5.1) Определить эффективную массу носителей
-заряда
-Из табл. 2 известно,
-что для полупроводника InSb эффективные
-массы электронов и «дырок» соответственно:
-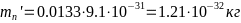 -
-и
-
-
-и
-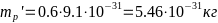 -.
-.
-
-5.2) Оценка степени вырождения электронного
-газа
-Зависимость энергии
-Ферми от температуры имеет следующий
-вид:
-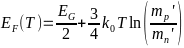 -,
-где
-
-,
-где
-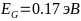 -
-— ширина запрещённой зоны. (отсчёт идёт
-от потолка валентной зоны (EC).
-Соответствующее выражение для тепловой
-энергии:
-
-
-— ширина запрещённой зоны. (отсчёт идёт
-от потолка валентной зоны (EC).
-Соответствующее выражение для тепловой
-энергии:
-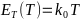 -.
-Их график представлен на рис. 17.
-.
-Их график представлен на рис. 17.
-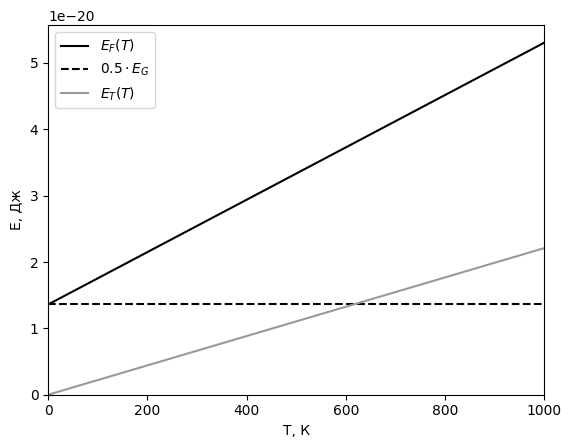 -
-
-Рис. 17 График
-температурной зависимости энергии
-Ферми и тепловой энергии
-Как видно из
-графика, критерий вырожденности
-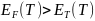 -
-выполняется для всех рассматриваемых
-температур, следовательно в этих
-условиях, электронный газ является
-вырожденным. Это значит, что он описывается
-распределением Ферми-Дирака:
-
-
-выполняется для всех рассматриваемых
-температур, следовательно в этих
-условиях, электронный газ является
-вырожденным. Это значит, что он описывается
-распределением Ферми-Дирака:
-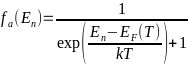 -.
-Например, для
-
-.
-Например, для
-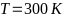 -,
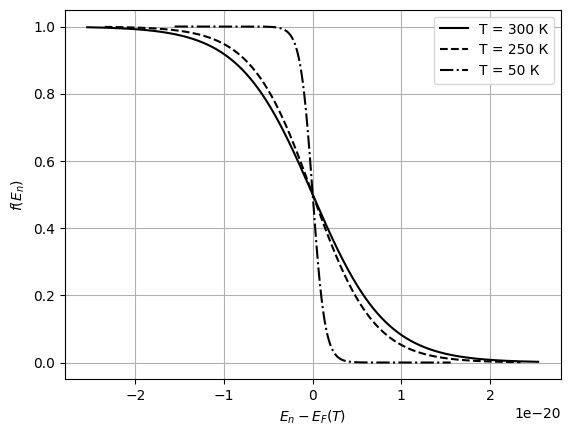
-распределение показано на рис. 18.
-,
-распределение показано на рис. 18.
- -
-
-Рис. 18
-Распределение Ферми-Дирака носителей
-заряда по энергиям при
-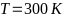 -
-
-
-5.3) Исследование зависимости концентрации
-носителей заряда от температуры для
-собственного полупроводника
-Зависимости
-концентрации электронов и дырок от
-температуры имеют следующий вид:
-
-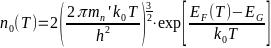 -
-
-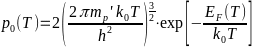 -
-
-Их график
-приведён на рис. 19.
-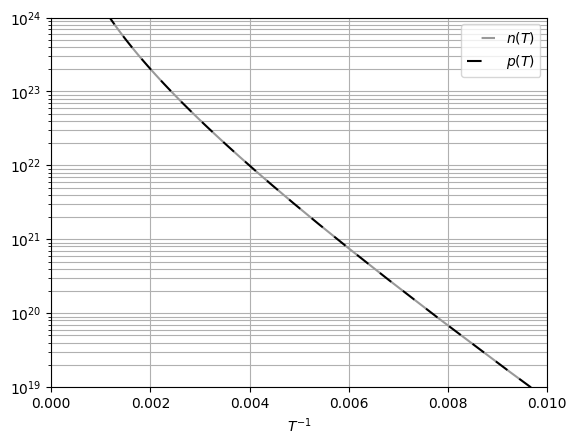 -
-
-Рис. 19 График
-зависимостей концентрации электронов
-и дырок от температуры
-
-5.4) Исследование зависимости концентрации
-носителей заряда от температуры для
-примесного полупроводника
-В работе рассмотрена
-донорная примесь Te с энергией ионизации
-в кристаллической решётке антимонида
-индия Eg = Ed
-= 0.003 эВ. Её концентрация Nd
-= 1022 м-3.
-Тогда, концентрация
-электронов в ней равна
-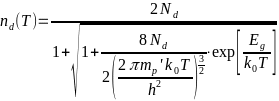 -
-
-Кроме этого, справедливы
-аппроксимации:
-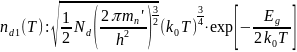 -
-
-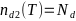 -
-
-Тогда полная концентрация
-электронов донорного полупроводника
-будет суммой концентраций собственного
-и полученных от донорной примеси.
-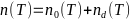 -
-
-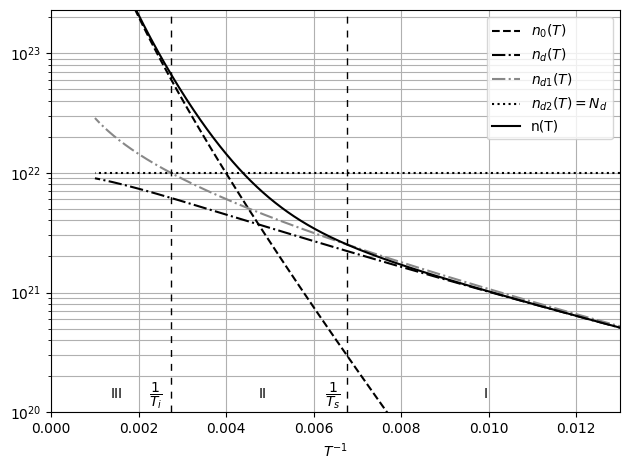 -
-
-Рис. 20 График
-зависимости концентрации зарядов в
-примесном проводнике от обратной
-температуры
-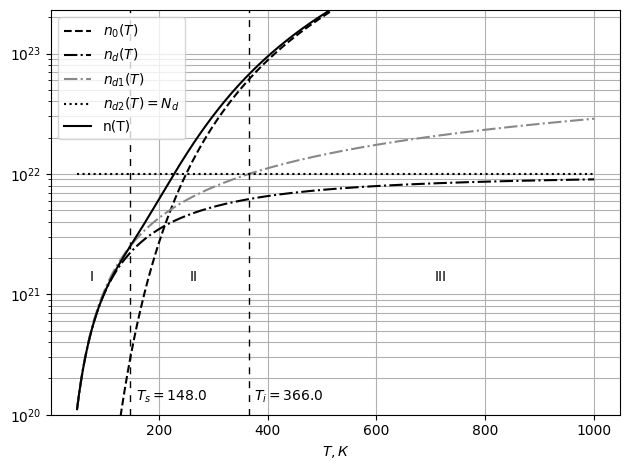 -
-
-Рис. 21 График
-зависимости концентрации зарядов в
-примесном проводнике от температуры
-По графику определяются
-температуры перехода к собственной
-проводимости и истощения примесей: Ts
-= 148 К (точка пересечения nd1(T)
-и n(T)) и Ti = 366 К
-(момент, когда nd1(T)
-становится больше Nd). Таким образом,
-I — область примесной ионизации, II —
-область истощения, III — область собственной
-ионизации.
-
-5.5) Исследование зависимости подвижности
-от температуры для примесного
-полупроводника
-Аппроксимирующие
-выражения для электронной и дырочной
-проводимостей:
-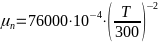 -,
-
-,
-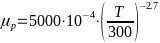 -,
-где
-
-,
-где
-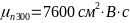 -
-и
-
-
-и
- -
-— подвижности при 300 К.
-
-— подвижности при 300 К.
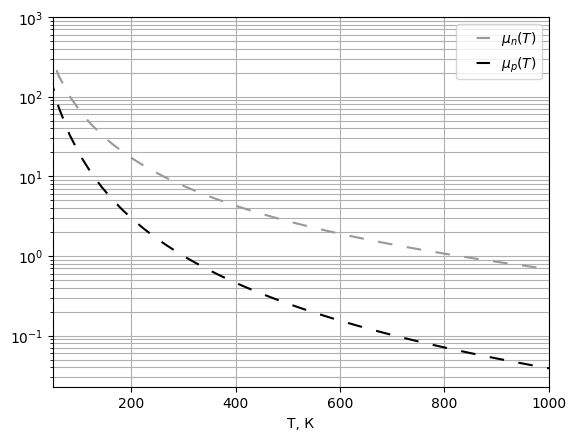
-Их график приведён на
-рис. 22.
- -
-
-Рис. 22 График
-подвижностей электронов и дырок
-
-5.6) Исследование зависимости
-электропроводности от температуры для
-примесного полупроводника
-Электропроводность
-проводника выражается следующим образом:
-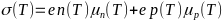 -,
-где p(T) — концентрация дырок из
-подпункта 5.3, а n(T) — суммарная
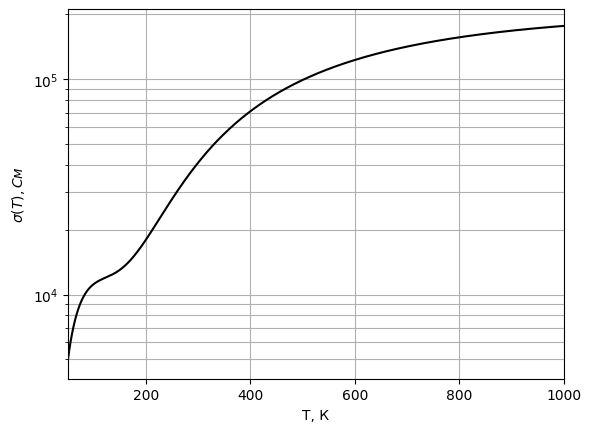
-концентрация электронов из 5.4. График
-приведён на рис. 23
-,
-где p(T) — концентрация дырок из
-подпункта 5.3, а n(T) — суммарная
-концентрация электронов из 5.4. График
-приведён на рис. 23
- -
-
-Рис. 23 График
-электропроводности примесного
-полупроводника
-
-Вывод: ввиду вырожденности, электронный
-газ описывается распределением
-Ферми-Дирака. В собственном полупроводнике
-количество электронов и дырок равно,
-поэтому зависимости концентраций
-совпадают. Добавление донорной примеси
-увеличивает концентрацию электронов,
-однако, с ростом температуры они
-истощаются и полупроводник переходит
-к собственной ионизации. С ростом
-температуры за счёт ионизации, а значит
-увеличения количества носителей заряда,
-в отличие от металла, проводимость
-полупроводника растёт.
-
-
-6) Рассчитать зависимости энергии Ферми
-и термодинамической работы выхода для
-примесного полупроводника от температуры.
-Термодинамическая
-работа выхода для собственного
-полупроводника определяется следующим
-выражением:
- -,
-где EF(T) — энергия Ферми
-из п. 5.2,
-
-,
-где EF(T) — энергия Ферми
-из п. 5.2,
-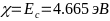 -
-- энергия сродства
-
-- энергия сродства
-Тогда расчёты
-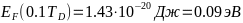 -;
-
-;
-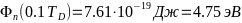 -
-
-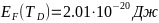 -;
-
-;
-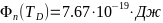 -
-
-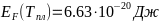 -;
-
-;
-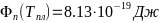 -
-
-Для примесного
-полупроводника, соответственно:
-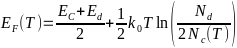 -
-и
-
-
-и
-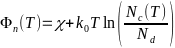 -,
-,
-где Ec =
-EG; Ed = Eg;
-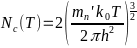 -
-
-И расчёты:
-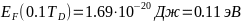 -;
-
-;
-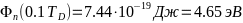 -
-
-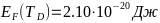 -;
-
-;
-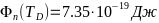 -
-
-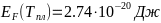 -;
-
-;
-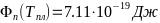 -
-
-Вывод: в примесном
-полупроводнике энергия Ферми и работа
-выхода меньше, чем в собственном, но в
-обоих случаях растут по мере возрастания
-температуры.
-
-
-
-
-7) Построить энергетическую диаграмму
-заданной пары металл-полупроводник в
-выбранном масштабе для случаев: без
-смещения, при прямом и обратном смещениях.
-Рассчитать вольтамперную характеристику
-контакта в данном диапазоне температур.
-
-7.1) Энергетическая диаграмма
-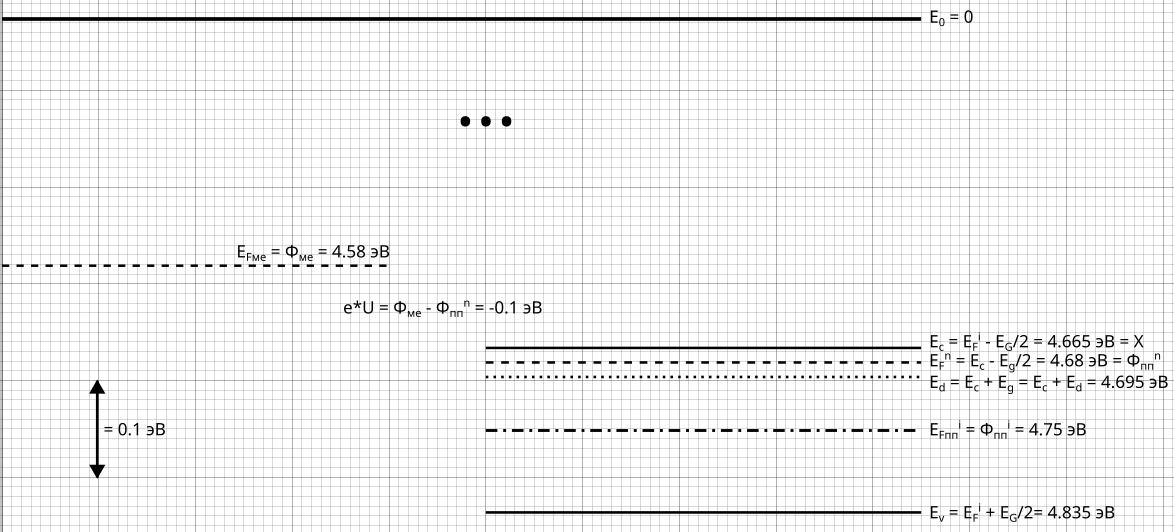 -
-
-Рис. 24
-Энергетическая диаграмма
-металл-вакуум-полупроводник
-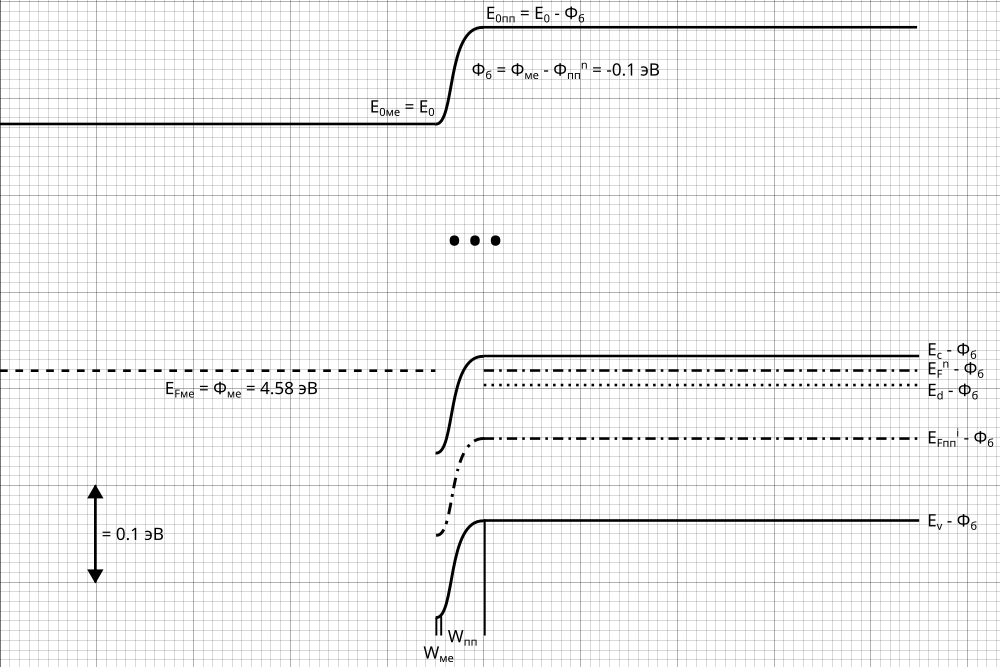 -
-
-Рис. 25
-Энергетическая диаграмма металл-полупроводник
-Вывод: Так
-как
-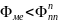 -,
-следовательно, наблюдается анти-барьер
-Шоттки, или омический контакт.
-,
-следовательно, наблюдается анти-барьер
-Шоттки, или омический контакт.
-
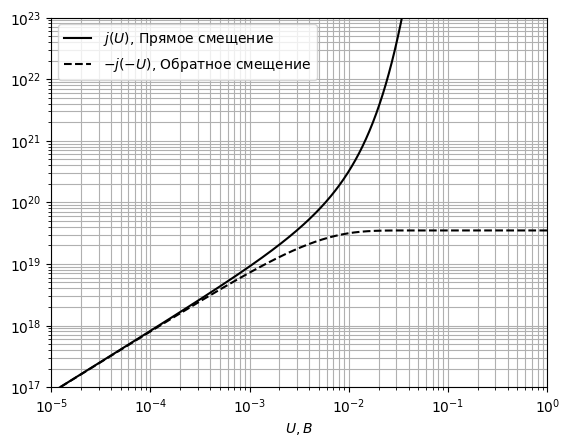
-7.2) Вольт-амперная характеристика
-В ходе построений было
-вычислено, что работа выхода из примесного
-полупроводника
- -,
-энергия контактной разности потенциалов
-
-
-,
-энергия контактной разности потенциалов
-
-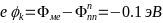 -.
-.
-Тогда, согласно
-уравнению Ричардсона, плотность тока
-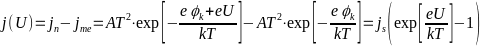 -.
-.
-Где
-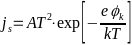 -
-- плотность тока насыщения.
-
-- плотность тока насыщения.
-Для трёх температур
-на рис. 28-30 приведены графики ВАХ.
-
-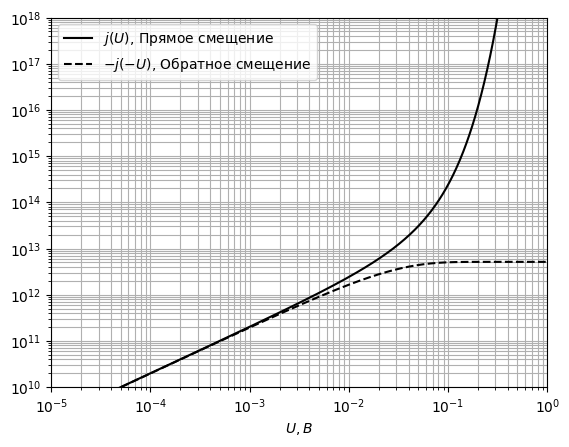 -
-
-Рис. 28 ВАХ
-контакта при T = 300 К
-
-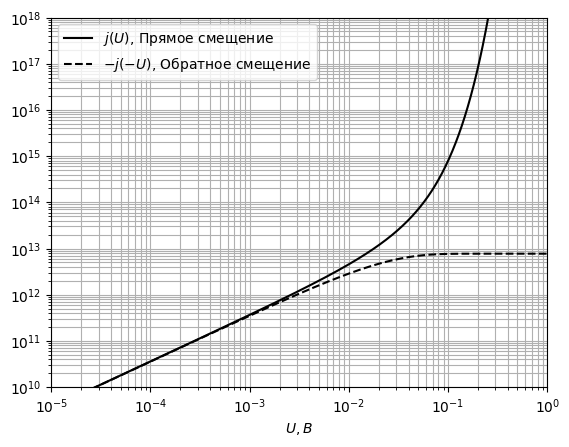 -
-
-
-Рис. 29 ВАХ контакта при T = 250 К
-
- -
-
-
-Рис. 30 ВАХ контакта при T = 50 К
-Вывод:
-анти-барьер Шоттки
-виден и на
-ВАХ, где в области
-небольших напряжений выполняется закон
-Ома. Сопротивление
-в ней определяется только
-сопротивлением
-приконтактной области
-полупроводника.
-
-
-
-
-8) Рассчитать концентрацию носителей
-заряда в заданном полупроводнике для
-создания омического контакта к металлу.
-Как видно из п. 7, контакт
-Au-InSb образует анти-барьер Шоттки, поэтому
-дополнительно легированный буферный
-слой не требуется.
-
-9) Сделать выводы и дать рекомендации
-по применению исследуемого контакта
-металл-полупроводник
-В работе были исследованы
-металл золото (Au) и полупроводник
-антимонид индия (InSb). Оба материала имеют
-гранецентрированную кристаллическую
-решётку, характеристики каждой были
-исследованы в п. 1.
-В п. 2 на основании
-вычисления концентрации свободных
-электронов было выяснено, что к металлу
-неприменима теория свободных электронов.
-Золото является хорошим
-проводником, что было подтверждено в
-п. 3, где была исследована температурная
-зависимость проводимости и связанные
-с ней характеристики и влияние на неё
-дефектов кристаллической решётки.
-При этом, как показано
-в п. 4, при толщине менее 60 нм начинает
-сказываться размерный эффект — при
-отражении на неровностях теряется
-импульс по направлению движения
-электронов, из-за чего сильно возрастает
-сопротивление.
-В п. 5 на основании
-заданных эффективных масс электронов
-и «дырок» было выяснено, что антимонид
-индия является вырожденным, а значит,
-должно использоваться распределение
-Ферми-Дирака. Однако, далее в расчётах
-использовались формулы для невырожденного
-случая. В собственном полупроводнике,
-действительно, концентрации электронов
-и «дырок» совпали.
-
-С добавлением донорной
-примеси теллура (Te) при низких температурах
-концентрация электронов возрастает за
-счёт ионизации примесей, однако, по мере
-роста температуры они истощаются и уже
-при 366 К их вклад становится пренебрежимо
-мал. Проводимость полупроводника на
-несколько порядков меньше, чем у металла
-и возрастает по мере роста температуры.
-В п. 6 было показано,
-что добавление примеси в полупроводник
-уменьшает работу выхода.
-На основании
-энергетических диаграмм, построенных
-в п. 7 было выяснено, что золото и антимонид
-индия, легированных теллуром образуют
-омический контакт с высотой барьера
-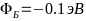 -
-и энергией сродства полупроводника
-
-
-и энергией сродства полупроводника
-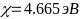 -.
-Поэтому на вольт-амперной характеристике
-при небольших напряжениях наблюдается
-прямой участок, подчиняющийся закону
-Ома. При этом, так как с ростом напряжении
-при прямом включении наблюдается
-значительный рост тока, а при обратном
-«запирание» диода.
-.
-Поэтому на вольт-амперной характеристике
-при небольших напряжениях наблюдается
-прямой участок, подчиняющийся закону
-Ома. При этом, так как с ростом напряжении
-при прямом включении наблюдается
-значительный рост тока, а при обратном
-«запирание» диода.
-Таким образом, полученный
-контакт можно использовать для соединения
-полупроводниковых приборов с металлическими
-выводами. Его удельное сопротивление
-получается порядка 10-14 Ом. Однако,
-уже при напряжениях порядка сотых долей
-вольта контакт становится выпрямляющим.
-
-Список литературы
-
-
- Ситникова
- М.В. Методические указания к решению
- задач на практических занятиях по
- дисциплине «Основы электроники и
- радиоматериалы», СпбГЭТУ «ЛЭТИ», 2021
-
- Астанин
- В.В. Электронное строение и кристаллическая
- структура твердых тел. Учебное пособие.
- / Уфа: УГАТУ, 2007,- 132с.
-
- Ашкрофт
- Н., Мермин Н. Физика твердого тела. Т.1.
- М.: Мир, 1979
-
- Гольдберг
- Ю.А. Омический контакт металл--полупроводник
- AIIIBV: методы создания и свойства // Физика
- и техника полупроводников. 1994, вып (№)
- 10. С. 1681-1689
-
-
-
-
\ No newline at end of file
diff --git a/README.md b/README.md
new file mode 100644
index 0000000..37bc62a
--- /dev/null
+++ b/README.md
@@ -0,0 +1,1846 @@
+**МИНОБРНАУКИ РОССИИ**
+
+**Санкт-Петербургский государственный**
+
+**электротехнический университет**
+
+**«ЛЭТИ» им. В.И. Ульянова (Ленина)**
+
+**Кафедра Микрорадиоэлектроники и технологии радиоаппаратуры**
+
+**(МИТ)**
+
+
+
+
+
+
+
+
+
+
+
+**ОТЧЕТ**
+
+**по ИДЗ**
+
+**по дисциплине «ОЭиР»**
+
+**Тема: Исследование
+контактных явлений в структуре
+металл-полупроводник**
+
+
+
+**Вариант
+****25****
+14,6,3**
+
+https://www.meme-arsenal.com/memes/4598e00877a721c55a46dc4aafb78719.jpg
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+Студент гр. 1181 |
+
+
|
+Шишков
+Д.А. |
+
+
+Преподаватель |
+
+
|
+Ситникова
+М.Ф. |
+
+
+
+
+
+
+
+
+
+
+Санкт-Петербург
+
+2023
+
+# Содержание
+
+[Задание 4](#__RefHeading___Toc9341_1004173995)
+
+[1) Определить класс симметрии заданных материалов, построить прямую и
+обратную элементарные ячейки заданных материалов. Определить размеры
+Зоны Бриллюэна в направлениях X, L, К.
+5](#__RefHeading___Toc9343_1004173995)
+
+[1.1) Металл — золото (Au): 5](#__RefHeading___Toc9345_1004173995)
+
+[1.2) Полупроводник - антимонид индия (InSb)
+8](#__RefHeading___Toc9347_1004173995)
+
+[2) Определить концентрацию электронов для заданного металла из условия
+касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости
+теории свободных электронов. 9](#__RefHeading___Toc9349_1004173995)
+
+[3) Рассчитать и построить зависимости средней длины свободного пробега,
+времени релаксации и электропроводности от температуры для металла в
+диапазоне температур (0,1 - 10) *Т**D*. Оценить степень
+дефектности металла по заданной величине удельного сопротивления.
+10](#__RefHeading___Toc9351_1004173995)
+
+[3.1) Исследование температурной зависимости длины свободного пробега
+10](#__RefHeading___Toc9353_1004173995)
+
+[3.2) Исследование влияния дефектов на время релаксации
+11](#__RefHeading___Toc9355_1004173995)
+
+[3.3) Исследование температурной зависимости электропроводности и
+теплопроводности металлов 13](#__RefHeading___Toc9357_1004173995)
+
+[3.4) Оценить степень дефектности металла по заданной величине удельного
+сопротивления 16](#__RefHeading___Toc9359_1004173995)
+
+[4) Рассчитать и построить зависимость
+электропроводности от толщины металлической пленки при заданной
+температуре. Определить минимально возможную толщину металлизации.
+17](#__RefHeading___Toc9365_1004173995)
+
+[5) Определить эффективную массу носителей заряда, их концентрацию и
+степень вырождения электронно-дырочного газа в заданном собственном
+полупроводнике в данном диапазоне температур. Рассчитать и построить
+зависимости концентрации, подвижности и электропроводности от
+температуры для заданного примесного полупроводника.
+19](#__RefHeading___Toc7584_2535136682)
+
+[5.1) Определить эффективную массу носителей заряда
+19](#__RefHeading___Toc7586_2535136682)
+
+[5.2) Оценка степени вырождения электронного газа
+19](#__RefHeading___Toc7588_2535136682)
+
+[5.3) Исследование зависимости концентрации носителей заряда от
+температуры для собственного полупроводника
+20](#__RefHeading___Toc7590_2535136682)
+
+[5.4) Исследование зависимости концентрации носителей заряда от
+температуры для примесного полупроводника
+21](#__RefHeading___Toc7592_2535136682)
+
+[5.5) Исследование зависимости подвижности от температуры для примесного
+полупроводника 23](#__RefHeading___Toc7951_3827154421)
+
+[5.6) Исследование зависимости электропроводности от температуры для
+примесного полупроводника 23](#__RefHeading___Toc7953_3827154421)
+
+[6) Рассчитать зависимости энергии Ферми и термодинамической работы
+выхода для примесного полупроводника от температуры.
+25](#__RefHeading___Toc7955_3827154421)
+
+[7) Построить энергетическую диаграмму заданной пары
+металл-полупроводник в выбранном масштабе для случаев: без смещения, при
+прямом и обратном смещениях. Рассчитать вольтамперную характеристику
+контакта в данном диапазоне температур.
+26](#__RefHeading___Toc7957_3827154421)
+
+[7.1) Энергетическая диаграмма 26](#__RefHeading___Toc7959_3827154421)
+
+[7.2) Вольт-амперная характеристика
+27](#__RefHeading___Toc7961_3827154421)
+
+[8) Рассчитать концентрацию носителей заряда в заданном полупроводнике
+для создания омического контакта к металлу.
+29](#__RefHeading___Toc3417_2577644421)
+
+[9) Сделать выводы и дать рекомендации по применению исследуемого
+контакта металл-полупроводник 30](#__RefHeading___Toc7965_3827154421)
+
+[Список литературы 32](#__RefHeading___Toc9363_1004173995)
+
+
+
+# Задание
+
+Для заданной пары металл-полупроводник оценить кинетические свойства
+заданных материалов, рассчитать и построить энергетическую диаграмму и
+вольт-амперную характеристику контакта в заданном диапазоне температур,
+дать рекомендации по применению исследуемого контакта.
+
+*Таблица 1. Некоторые свойства металлов*
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+No
+ВАР. |
+Элемент |
+Структура |
+Атомная
+масса |
+Параметр
+решетки, Å |
+Плотность,
+г/см3 |
+Удельное
+сопротивление, мкОм·см |
+Температура,
+К |
+Работа выхода φ,
+эВ |
+
+
+Дебая
+(TD) |
+Ферми
+(TF·10-4) |
+плавления
+(Tпл) |
+
+
+14 |
+Au |
+ГЦК |
+196.9 |
+4.08 |
+19.28 |
+2.2 |
+165 |
+6.39 |
+1337 |
+4.58 |
+
+
+
+
+
+
+*Таблица 2. Свойства cобственных полупроводников*
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+№
+ВАР. |
+Тип
+примеси |
+Полупроводник |
+Ширина
+запрещённой области |
+Эффективная
+масса |
+Подвижность
+при 300К |
+Работа выхода,
+Эв |
+
+
+EG
+(300 К), Эв |
+m"n/me |
+m’’p/me |
+μn,
+см2·В1·с1 |
+μp,
+см2·В1·с1 |
+
+
+6 |
+n |
+InSb |
+0.17 |
+0.0133 |
+0.6 |
+76000 |
+5000 |
+4.75 |
+
+
+
+
+
+
+*Таблица 3. Концентрация n- и p- примесей в полупроводниках*
+
+
+
+
+
+
+
+
+№
+вар. |
+3 |
+
+
+концентрация
+примесей, м-3 |
+1022 |
+
+
+
+
+
+
+
+
+# 1) Определить класс симметрии заданных материалов, построить прямую и обратную элементарные ячейки заданных материалов. Определить размеры Зоны Бриллюэна в направлениях X, L, К.
+
+## 1.1) Металл — золото (Au):
+
+Структура: Гранецентрированная кубическая решётка
+
+Формула симметрии: 3L44L36L29PC
+
+Класс симметрии: m3m
+
+Так как формулы симметрии ГЦК и простой кубической решётки совпадают, на
+рис. 1-3 приведены изображения осей, плоскостей и центра симметрии для
+последнего
+
+![]() +
+Рис. 1 Изображение осей симметрии кубической решётки
+
+
+
+
+
+Рис. 1 Изображение осей симметрии кубической решётки
+
+
+
+![]() +
+Рис. 2 Изображение плоскостей симметрии куба
+
+
+
+Рис. 2 Изображение плоскостей симметрии куба
+
+![]() +
+Рис. 3 Изображение центра симметрии куба
+
+Базисные вектора:
+
+
+
+Рис. 3 Изображение центра симметрии куба
+
+Базисные вектора:
+
+![]() ,
, ![]() ,
, ![]() +
+Подставляя параметр решётки
+
+Подставляя параметр решётки ![]() +
+
+
+![]() ,
, ![]() ,
, ![]() +
+Кристаллическая решётка по заданным векторам построена на рис. 4
+
+
+
+Кристаллическая решётка по заданным векторам построена на рис. 4
+
+![]() +
+Рис. 4 Тройка основных векторов для ГЦК решётки
+
+Объём элементарной ячейки:
+
+
+
+Рис. 4 Тройка основных векторов для ГЦК решётки
+
+Объём элементарной ячейки:
+
+![]() +
+Базисные вектора обратной решётки:
+
+
+
+Базисные вектора обратной решётки:
+
+![]() ;
; ![]() +
+
+
+![]() ,
, ![]() ,
, ![]() +
+Что соответствует ОЦК. Её изображение на рис. 5.
+
+
+
+Что соответствует ОЦК. Её изображение на рис. 5.
+
+![]() +
+Рис. 5 Обратная решётка для ГЦК — ОЦК
+
+Первая зона Бриллюэна (рис. 6):
+
+
+
+Рис. 5 Обратная решётка для ГЦК — ОЦК
+
+Первая зона Бриллюэна (рис. 6):
+
+![]() +
+Рис. 6 Первая зона Бриллюэна
+
+Размеры зоны Бриллюэна по направлениям X, L, K:
+
+
+
+Рис. 6 Первая зона Бриллюэна
+
+Размеры зоны Бриллюэна по направлениям X, L, K:
+
+![]() - центр верхнего квадрата, по
+направлению \[001\]
+
+
- центр верхнего квадрата, по
+направлению \[001\]
+
+![]() - центр шестиугольника, по
+направлению \[111\]
+
+
- центр шестиугольника, по
+направлению \[111\]
+
+![]() - середина грани соединяющей
+два шестиугольника, по направлению \[101\]
+
+## 1.2) Полупроводник - антимонид индия (InSb)
+
+
- середина грани соединяющей
+два шестиугольника, по направлению \[101\]
+
+## 1.2) Полупроводник - антимонид индия (InSb)
+
+![]() +
+Рис. 7 Антимонид индия
+
+Структура: Гранецентрированная кубическая решётка
+
+Формула симметрии: 3L44L36L29PC
+
+Класс симметрии: m3m
+
+Изображения осей, плоскостей и центра симметрии для последнего — см.
+рис. 1-3.
+
+Базисные вектора:
+
+
+
+Рис. 7 Антимонид индия
+
+Структура: Гранецентрированная кубическая решётка
+
+Формула симметрии: 3L44L36L29PC
+
+Класс симметрии: m3m
+
+Изображения осей, плоскостей и центра симметрии для последнего — см.
+рис. 1-3.
+
+Базисные вектора:
+
+![]() ,
, ![]() ,
, ![]() , считая, что постоянная решётки
+= 1
+
+Для параметра решётки
, считая, что постоянная решётки
+= 1
+
+Для параметра решётки ![]() +
+
+
+![]() ,
, ![]() ,
, ![]() +
+Кристаллическая решётка по заданным векторам изображена на рис. 4.
+
+Объём элементарной ячейки аналогично предыдущему пункту:
+
+
+
+Кристаллическая решётка по заданным векторам изображена на рис. 4.
+
+Объём элементарной ячейки аналогично предыдущему пункту:
+
+![]() +
+Базисные вектора в обратном пространстве:
+
+
+
+Базисные вектора в обратном пространстве:
+
+![]() ;
; ![]() +
+
+
+![]() ,
, ![]() ,
, ![]() +
+
+
+# 2) Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов.
+
+Связь радиуса Ферми с концентрацией электронов можно выяснить из
+следующего выражения:
+
+
+
+# 2) Определить концентрацию электронов для заданного металла из условия касания зоны Бриллюэна и сферы Ферми и сделать суждение о применимости теории свободных электронов.
+
+Связь радиуса Ферми с концентрацией электронов можно выяснить из
+следующего выражения: ![]() . С другой стороны введено условие касания сферы Ферми
+с границей зоны Бриллюэна. Из п. 1 известно, что наименьшие размеры она
+имеет по направлению *
. С другой стороны введено условие касания сферы Ферми
+с границей зоны Бриллюэна. Из п. 1 известно, что наименьшие размеры она
+имеет по направлению *![]() * , следовательно радиус Ферми для вписанной сферы
* , следовательно радиус Ферми для вписанной сферы ![]() +
+Тогда концентрация электронов:
+
+Тогда концентрация электронов: ![]() +
+Концентрацию свободных электронов в металле также можно определить
+пользуясь приближением слабой связи для:
+
+
+
+Концентрацию свободных электронов в металле также можно определить
+пользуясь приближением слабой связи для:
+
+![]() , где Z — его валентность, N —
+количество атомов в его элементарной ячейке, а V — её объём.
+
+Для золота:
+
+В элементарной ГЦК решётке N = 4 атома (см. рис. 8)
+
+
, где Z — его валентность, N —
+количество атомов в его элементарной ячейке, а V — её объём.
+
+Для золота:
+
+В элементарной ГЦК решётке N = 4 атома (см. рис. 8)
+
+![]() +
+Рис. 8 Атомы элементарной ячейки ГЦК решётки
+
+При Z = 1
+
+Рис. 8 Атомы элементарной ячейки ГЦК решётки
+
+При Z = 1 ![]() +
+При Z = 2
+
+При Z = 2 ![]() +
+При Z = 3
+
+При Z = 3 ![]() - наиболее частая
+
+*Вывод:* Как видно,
- наиболее частая
+
+*Вывод:* Как видно, ![]() для любой возможной валентности,
+следовательно, теория свободных электронов не применима. Тогда
+эффективную массу электрона примем равной массе свободного электрона
+
для любой возможной валентности,
+следовательно, теория свободных электронов не применима. Тогда
+эффективную массу электрона примем равной массе свободного электрона
+![]() кг. В сравнении со стандартным
+металлом Пиппарда, у которого плотность электронов
кг. В сравнении со стандартным
+металлом Пиппарда, у которого плотность электронов ![]() , а радиус Ферми
, а радиус Ферми ![]() , у золота они получаются
+большими
, у золота они получаются
+большими ![]() ,
, ![]() .
+
+# 3) Рассчитать и построить зависимости средней длины свободного пробега, времени релаксации и электропроводности от температуры для металла в диапазоне температур (0,1 - 10) *Т**D*. Оценить степень дефектности металла по заданной величине удельного сопротивления.
+
+## 3.1) Исследование температурной зависимости длины свободного пробега
+
+Длина свободного пробега электронов в зависимости от температуры (если
+она много больше температуры Дебая, то происходит упругое рассеяние,
+иначе - неупругое) приблизительно рассчитывается согласно следующему
+выражению:
+
+
.
+
+# 3) Рассчитать и построить зависимости средней длины свободного пробега, времени релаксации и электропроводности от температуры для металла в диапазоне температур (0,1 - 10) *Т**D*. Оценить степень дефектности металла по заданной величине удельного сопротивления.
+
+## 3.1) Исследование температурной зависимости длины свободного пробега
+
+Длина свободного пробега электронов в зависимости от температуры (если
+она много больше температуры Дебая, то происходит упругое рассеяние,
+иначе - неупругое) приблизительно рассчитывается согласно следующему
+выражению:
+
+![]() .
+
+Где
.
+
+Где ![]() ,
, ![]() — параметр решётки,
— параметр решётки, ![]() — температура плавления
— температура плавления ![]() — температура Дебая.
+
+
— температура Дебая.
+
+![]() ,
, ![]() ,
, ![]() +
+
+
+![]() +
+Рис. 9 График зависимости длин свободного пробега от температуры
+
+*Вывод:* с ростом температуры длина свободного пробега действительно
+уменьшается.
+
+## 3.2) Исследование влияния дефектов на время релаксации
+
+Время релаксации для рассеивания на дефектах:
+
+Рис. 9 График зависимости длин свободного пробега от температуры
+
+*Вывод:* с ростом температуры длина свободного пробега действительно
+уменьшается.
+
+## 3.2) Исследование влияния дефектов на время релаксации
+
+Время релаксации для рассеивания на дефектах: ![]() +
+Время релаксации для электрон-фононного
+рассеивания
+в
+зависимости от температуры:
+
+Время релаксации для электрон-фононного
+рассеивания
+в
+зависимости от температуры: ![]() , где
, где ![]() — скорость электронов на поверхности Ферми.
+В последней
+формуле
— скорость электронов на поверхности Ферми.
+В последней
+формуле ![]() — постоянная Планка,
— постоянная Планка, ![]() — концентрация
+носителей
+заряда,
— концентрация
+носителей
+заряда, ![]() — эффективная масса
+электрона.
+
+Тогда, согласно правилу Маттиссена суммарное время релаксации получается
+следующим:
— эффективная масса
+электрона.
+
+Тогда, согласно правилу Маттиссена суммарное время релаксации получается
+следующим: ![]() .
+
+Оно справедливо если
+один
+из
+механизмов рассеяния
+преобладает
+над другим
+при
+*T *=
+273 *К*.
+
+
.
+
+Оно справедливо если
+один
+из
+механизмов рассеяния
+преобладает
+над другим
+при
+*T *=
+273 *К*.
+
+![]() ;
; ![]() ;
; ![]() +
+Воспользуемся формулой для электропроводности:
+
+Воспользуемся формулой для электропроводности: ![]() , где
, где ![]() — заряд электрона,
— заряд электрона, ![]() — удельное сопротивление золота при
+Н.У.
— удельное сопротивление золота при
+Н.У. ![]() .
+
+Подставив эти значения в правило
+Маттиссена,
+получим
.
+
+Подставив эти значения в правило
+Маттиссена,
+получим ![]() .
+
+*В**ывод:*
+преобладает механизм
+рассеивания на дефектах,
+так как его
+время релаксации меньше.
+В сравнении
+со
+стандартным металлом Пиппарда, у которого скорость электронов на
+поверхности Ферми
.
+
+*В**ывод:*
+преобладает механизм
+рассеивания на дефектах,
+так как его
+время релаксации меньше.
+В сравнении
+со
+стандартным металлом Пиппарда, у которого скорость электронов на
+поверхности Ферми ![]() , у золота она выше:
, у золота она выше: ![]() .
+
+Построим график зависимости
+времени
+релаксации
+от
+температуры
+для
+обоих
+механизмов рассеивания и суммарный, считая что на дефектах оно будет постоянным.
+
+
.
+
+Построим график зависимости
+времени
+релаксации
+от
+температуры
+для
+обоих
+механизмов рассеивания и суммарный, считая что на дефектах оно будет постоянным.
+
+![]() +
+Рис. 10 График зависимости времени релаксации
+от
+температуры
+
+Для разных температур и времён релаксации для рассеяния на дефектах вычислим общее время релаксации
+по
+правилу
+Маттиссена:
+
+*Таблица 4. Суммарное время релаксации
+
+
+Рис. 10 График зависимости времени релаксации
+от
+температуры
+
+Для разных температур и времён релаксации для рассеяния на дефектах вычислим общее время релаксации
+по
+правилу
+Маттиссена:
+
+*Таблица 4. Суммарное время релаксации
+ ![]() *
+
+
*
+
+
+
+
+
+
+
+
+
+
+![]() \T \T
|
+![]()
|
+TD |
+Tпл |
+
+
+10-12 |
+10-12 |
+![]()
|
+![]()
|
+
+
+10-13 |
+10-13 |
+![]()
|
+![]()
|
+
+
+10-14 |
+10-14 |
+![]()
|
+![]()
|
+
+
+
+
+
+
+*Вывод:* С ростом температуры суммарное время релаксации уменьшается.
+
+## 3.3) Исследование температурной зависимости электропроводности и теплопроводности металлов
+
+Теплопроводность металла можно определить
+исходя из
+закона Видемана-Франца: ![]() , где
, где ![]() — число Лоренца, в чьей формуле присутствует
+
— число Лоренца, в чьей формуле присутствует
+ ![]() — постоянная
+Больцмана,
+а
— постоянная
+Больцмана,
+а ![]() — электропроводность, выраженная через время
+релаксации из предыдущего подпункта.
+
+Для разных температур и времён релаксации для рассеяния на дефектах
+вычислим электропроводность и теплопроводность:
+
+*Таблица 5. Значения
+электропроводности
— электропроводность, выраженная через время
+релаксации из предыдущего подпункта.
+
+Для разных температур и времён релаксации для рассеяния на дефектах
+вычислим электропроводность и теплопроводность:
+
+*Таблица 5. Значения
+электропроводности ![]() *
+
+
*
+
+
+
+
+
+
+
+
+
+
+![]() \T \T
|
+![]()
|
+TD |
+Tпл |
+
+
+10-12 |
+![]()
|
+![]()
|
+![]()
|
+
+
+10-13 |
+![]()
|
+![]()
|
+![]()
|
+
+
+10-14 |
+![]()
|
+![]()
|
+![]()
|
+
+
+
+
+
+
+*Таблица 6. Значения
+иеплопроводности ![]() *
+
+
*
+
+
+
+
+
+
+
+
+
+
+![]() \T \T
|
+![]()
|
+TD |
+Tпл |
+
+
+10-12 |
+![]()
|
+![]()
|
+![]()
|
+
+
+10-13 |
+805 |
+![]()
|
+![]()
|
+
+
+10-14 |
+80.5 |
+675 |
+![]()
|
+
+
+
+
+
+
+Изобразим их на графиках:
+
+![]() +
+Рис. 11
+Графики
+зависимости электропроводности и
+теплопроводности при
+
+Рис. 11
+Графики
+зависимости электропроводности и
+теплопроводности при ![]() +
+
+
+![]() +
+Рис. 12 Графики
+зависимости электропроводности и
+теплопроводности при
+
+Рис. 12 Графики
+зависимости электропроводности и
+теплопроводности при ![]() +
+
+
+![]() +
+Рис. 13 Графики
+зависимости электропроводности и
+теплопроводности при
+
+Рис. 13 Графики
+зависимости электропроводности и
+теплопроводности при ![]() +
+
+
+![]() +
+Рис. 14 Графики электропроводностей и теплопроводностей
+при различных
+
+Рис. 14 Графики электропроводностей и теплопроводностей
+при различных ![]() +
+*Вывод:* С ростом концентрации дефектов (
+
+*Вывод:* С ростом концентрации дефектов (![]() )
+температурные зависимости
+электропроводности и
+теплопроводности «выпрямляются», вместе с чем также уменьшается их значение в каждой точке. При
+этом, с ростом температуры электропроводность убывает, а теплопроводность возрастает.
+
+## 3.4) Оценить степень дефектности металла по заданной величине удельного сопротивления
+
+Как было вычислено в подпункте 3.2, время релаксации для рассеивания на
+дефектах
)
+температурные зависимости
+электропроводности и
+теплопроводности «выпрямляются», вместе с чем также уменьшается их значение в каждой точке. При
+этом, с ростом температуры электропроводность убывает, а теплопроводность возрастает.
+
+## 3.4) Оценить степень дефектности металла по заданной величине удельного сопротивления
+
+Как было вычислено в подпункте 3.2, время релаксации для рассеивания на
+дефектах ![]() . Тогда количество дефектов в
+металле
. Тогда количество дефектов в
+металле ![]() .
+
+*Вывод:* В сравнении с концентрацией носителей заряда
.
+
+*Вывод:* В сравнении с концентрацией носителей заряда ![]() , количество дефектов меньше на 10 порядков, что можно назвать приемлемым
+значением.
+
+
+
+# 4) Рассчитать и построить зависимость электропроводности от толщины металлической пленки при заданной температуре. Определить минимально возможную толщину металлизации.
+
+Графики зависимости электропроводности плёнки от толщины
, количество дефектов меньше на 10 порядков, что можно назвать приемлемым
+значением.
+
+
+
+# 4) Рассчитать и построить зависимость электропроводности от толщины металлической пленки при заданной температуре. Определить минимально возможную толщину металлизации.
+
+Графики зависимости электропроводности плёнки от толщины ![]() будут построены для двух
+значений параметра зеркальности *p*1 = 0 и *p*2 =
+0.5 в диапазоне температур
будут построены для двух
+значений параметра зеркальности *p*1 = 0 и *p*2 =
+0.5 в диапазоне температур ![]() .
+
+В предыдущем пункте при *T = T**пл* — температуре плавления
+была рассчитана длина свободного пробега
.
+
+В предыдущем пункте при *T = T**пл* — температуре плавления
+была рассчитана длина свободного пробега ![]() . Удельное сопротивление
+объёмного образца
. Удельное сопротивление
+объёмного образца ![]() .
+
+Для «толстой плёнки» при параметре зеркальности *p* < 1 справедлива
+следующая формула:
.
+
+Для «толстой плёнки» при параметре зеркальности *p* < 1 справедлива
+следующая формула: ![]() . Аналогично, для «тонкой
+плёнки»
. Аналогично, для «тонкой
+плёнки» ![]() :
: ![]() , где
, где ![]() +
+
+
+![]() +
+Рис. 15 График удельного сопротивления от толщины плёнки при параметре
+зеркальности 0
+
+
+
+Рис. 15 График удельного сопротивления от толщины плёнки при параметре
+зеркальности 0
+
+![]() +
+Рис. 16 График удельного сопротивления от толщины плёнки при параметре
+зеркальности 0.5
+
+При p = 1 (весь импульс электрона по направлению тока сохраняется),
+размерный эффект отсутствует
+
+Минимальную возможную толщину металлизации можно определить из
+вышеприведённых графиков, выбрав такую
+
+Рис. 16 График удельного сопротивления от толщины плёнки при параметре
+зеркальности 0.5
+
+При p = 1 (весь импульс электрона по направлению тока сохраняется),
+размерный эффект отсутствует
+
+Минимальную возможную толщину металлизации можно определить из
+вышеприведённых графиков, выбрав такую ![]() , что при заданном масштабе
+
, что при заданном масштабе
+![]() практически сольётся с
практически сольётся с ![]() . Для данного металла это будет
+
. Для данного металла это будет
+![]() . Тогда толщина
. Тогда толщина ![]() +
+*Вывод:* тонкие плёнки обладают низкой электропроводностью, однако, уже
+начиная с толщины
+
+*Вывод:* тонкие плёнки обладают низкой электропроводностью, однако, уже
+начиная с толщины ![]() плёнка из золота должна
+демонстрировать металлические свойства. При этом, при большем
+коэффициенте зеркальности поверхности, действительно, удельное
+сопротивление по мере уменьшения толщины плёнки возрастает в меньшей
+степени.
+
+
+
+# 5) Определить эффективную массу носителей заряда, их концентрацию и степень вырождения электронно-дырочного газа в заданном собственном полупроводнике в данном диапазоне температур. Рассчитать и построить зависимости концентрации, подвижности и электропроводности от температуры для заданного примесного полупроводника.
+
+## 5.1) Определить эффективную массу носителей заряда
+
+Из табл. 2 известно, что для полупроводника InSb эффективные массы
+электронов и «дырок» соответственно:
+
+
плёнка из золота должна
+демонстрировать металлические свойства. При этом, при большем
+коэффициенте зеркальности поверхности, действительно, удельное
+сопротивление по мере уменьшения толщины плёнки возрастает в меньшей
+степени.
+
+
+
+# 5) Определить эффективную массу носителей заряда, их концентрацию и степень вырождения электронно-дырочного газа в заданном собственном полупроводнике в данном диапазоне температур. Рассчитать и построить зависимости концентрации, подвижности и электропроводности от температуры для заданного примесного полупроводника.
+
+## 5.1) Определить эффективную массу носителей заряда
+
+Из табл. 2 известно, что для полупроводника InSb эффективные массы
+электронов и «дырок» соответственно:
+
+![]() и
и ![]() .
+
+## 5.2) Оценка степени вырождения электронного газа
+
+Зависимость энергии Ферми от температуры имеет следующий вид:
.
+
+## 5.2) Оценка степени вырождения электронного газа
+
+Зависимость энергии Ферми от температуры имеет следующий вид: ![]() , где
, где ![]() — ширина запрещённой зоны.
+(отсчёт идёт от потолка валентной зоны (*E**C*).
+Соответствующее выражение для тепловой энергии:
— ширина запрещённой зоны.
+(отсчёт идёт от потолка валентной зоны (*E**C*).
+Соответствующее выражение для тепловой энергии: ![]() . Их график представлен на рис.
+17.
+
+
. Их график представлен на рис.
+17.
+
+![]() +
+Рис. 17 График температурной зависимости энергии Ферми и тепловой
+энергии
+
+Как видно из графика, критерий вырожденности
+
+Рис. 17 График температурной зависимости энергии Ферми и тепловой
+энергии
+
+Как видно из графика, критерий вырожденности ![]() выполняется для всех
+рассматриваемых температур, следовательно в этих условиях, электронный
+газ является вырожденным. Это значит, что он описывается распределением
+Ферми-Дирака:
выполняется для всех
+рассматриваемых температур, следовательно в этих условиях, электронный
+газ является вырожденным. Это значит, что он описывается распределением
+Ферми-Дирака: ![]() . Например, для
. Например, для ![]() , распределение показано на
+рис. 18.
+
+
, распределение показано на
+рис. 18.
+
+![]() +
+Рис. 18 Распределение Ферми-Дирака носителей заряда по энергиям при
+
+Рис. 18 Распределение Ферми-Дирака носителей заряда по энергиям при ![]() +
+## 5.3) Исследование зависимости концентрации носителей заряда от температуры для собственного полупроводника
+
+Зависимости концентрации электронов и дырок от температуры имеют
+следующий вид:
+
+
+
+## 5.3) Исследование зависимости концентрации носителей заряда от температуры для собственного полупроводника
+
+Зависимости концентрации электронов и дырок от температуры имеют
+следующий вид:
+
+![]() +
+
+
+![]() +
+Их график приведён на рис. 19.
+
+
+
+Их график приведён на рис. 19.
+
+![]() +
+Рис. 19 График зависимостей концентрации электронов и дырок от
+температуры
+
+## 5.4) Исследование зависимости концентрации носителей заряда от температуры для примесного полупроводника
+
+В работе рассмотрена донорная примесь Te с энергией ионизации в
+кристаллической решётке антимонида индия *E**g* =
+*E**d* = 0.003 *эВ*. Её концентрация *N**d* =
+1022 *м*-3.
+
+Тогда, концентрация электронов в ней равна
+
+Рис. 19 График зависимостей концентрации электронов и дырок от
+температуры
+
+## 5.4) Исследование зависимости концентрации носителей заряда от температуры для примесного полупроводника
+
+В работе рассмотрена донорная примесь Te с энергией ионизации в
+кристаллической решётке антимонида индия *E**g* =
+*E**d* = 0.003 *эВ*. Её концентрация *N**d* =
+1022 *м*-3.
+
+Тогда, концентрация электронов в ней равна ![]() +
+Кроме этого, справедливы аппроксимации:
+
+
+
+Кроме этого, справедливы аппроксимации:
+
+![]() +
+
+
+![]() +
+Тогда полная концентрация электронов донорного полупроводника будет
+суммой концентраций собственного и полученных от донорной примеси.
+
+
+
+Тогда полная концентрация электронов донорного полупроводника будет
+суммой концентраций собственного и полученных от донорной примеси.
+
+![]() +
+
+
+![]() +
+Рис. 20 График зависимости концентрации зарядов в примесном проводнике
+от обратной температуры
+
+
+
+Рис. 20 График зависимости концентрации зарядов в примесном проводнике
+от обратной температуры
+
+![]() +
+Рис. 21 График зависимости концентрации зарядов в примесном проводнике
+от температуры
+
+По графику определяются температуры перехода к собственной проводимости
+и истощения примесей: *T**s* = 148 *К* (точка пересечения
+*n**d*1(*T*) и *n*(*T*)) и *T**i* = 366 *К*
+(момент, когда *n**d1*(*T*) становится больше Nd).
+Таким образом, I — область примесной ионизации, II — область истощения,
+III — область собственной ионизации.
+
+## 5.5) Исследование зависимости подвижности от температуры для примесного полупроводника
+
+Аппроксимирующие выражения для электронной и дырочной проводимостей:
+
+
+
+Рис. 21 График зависимости концентрации зарядов в примесном проводнике
+от температуры
+
+По графику определяются температуры перехода к собственной проводимости
+и истощения примесей: *T**s* = 148 *К* (точка пересечения
+*n**d*1(*T*) и *n*(*T*)) и *T**i* = 366 *К*
+(момент, когда *n**d1*(*T*) становится больше Nd).
+Таким образом, I — область примесной ионизации, II — область истощения,
+III — область собственной ионизации.
+
+## 5.5) Исследование зависимости подвижности от температуры для примесного полупроводника
+
+Аппроксимирующие выражения для электронной и дырочной проводимостей:
+
+![]() ,
, ![]() , где
, где ![]() и
и ![]() — подвижности при 300 К.
+
+Их график приведён на рис. 22.
+
+
— подвижности при 300 К.
+
+Их график приведён на рис. 22.
+
+![]() +
+Рис. 22 График подвижностей электронов и дырок
+
+## 5.6) Исследование зависимости электропроводности от температуры для примесного полупроводника
+
+Электропроводность проводника выражается следующим образом:
+
+
+
+Рис. 22 График подвижностей электронов и дырок
+
+## 5.6) Исследование зависимости электропроводности от температуры для примесного полупроводника
+
+Электропроводность проводника выражается следующим образом:
+
+![]() , где *p*(*T*) — концентрация
+дырок из подпункта 5.3, а *n*(*T*) — суммарная концентрация электронов
+из 5.4. График приведён на рис. 23
+
+
, где *p*(*T*) — концентрация
+дырок из подпункта 5.3, а *n*(*T*) — суммарная концентрация электронов
+из 5.4. График приведён на рис. 23
+
+![]() +
+Рис. 23 График электропроводности примесного полупроводника
+
+ *Вывод*: ввиду
+вырожденности, электронный газ описывается распределением Ферми-Дирака.
+В собственном полупроводнике количество электронов и дырок равно,
+поэтому зависимости концентраций совпадают. Добавление донорной примеси
+увеличивает концентрацию электронов, однако, с ростом температуры они
+истощаются и полупроводник переходит к собственной ионизации. С ростом
+температуры за счёт ионизации, а значит увеличения количества носителей
+заряда, в отличие от металла, проводимость полупроводника растёт.
+
+# 6) Рассчитать зависимости энергии Ферми и термодинамической работы выхода для примесного полупроводника от температуры.
+
+Термодинамическая работа выхода для собственного полупроводника
+определяется следующим выражением:
+
+
+
+Рис. 23 График электропроводности примесного полупроводника
+
+ *Вывод*: ввиду
+вырожденности, электронный газ описывается распределением Ферми-Дирака.
+В собственном полупроводнике количество электронов и дырок равно,
+поэтому зависимости концентраций совпадают. Добавление донорной примеси
+увеличивает концентрацию электронов, однако, с ростом температуры они
+истощаются и полупроводник переходит к собственной ионизации. С ростом
+температуры за счёт ионизации, а значит увеличения количества носителей
+заряда, в отличие от металла, проводимость полупроводника растёт.
+
+# 6) Рассчитать зависимости энергии Ферми и термодинамической работы выхода для примесного полупроводника от температуры.
+
+Термодинамическая работа выхода для собственного полупроводника
+определяется следующим выражением:
+
+![]() , где *E**F*(*T*) —
+энергия Ферми из п. 5.2,
, где *E**F*(*T*) —
+энергия Ферми из п. 5.2, ![]() - энергия сродства
+
+Тогда расчёты
+
+
- энергия сродства
+
+Тогда расчёты
+
+![]() ;
; ![]() +
+
+
+![]() ;
; ![]() +
+
+
+![]() ;
; ![]() +
+Для примесного полупроводника, соответственно:
+
+
+
+Для примесного полупроводника, соответственно:
+
+![]() и
и ![]() ,
+
+где *E**c* = *E**G*; *E**d* =
+*E**g*;
,
+
+где *E**c* = *E**G*; *E**d* =
+*E**g*; ![]() +
+И расчёты:
+
+
+
+И расчёты:
+
+![]() ;
; ![]() +
+
+
+![]() ;
; ![]() +
+
+
+![]() ;
; ![]() +
+Вывод: в примесном полупроводнике энергия Ферми и работа выхода меньше,
+чем в собственном, но в обоих случаях растут по мере возрастания
+температуры.
+
+#
+
+# 7) Построить энергетическую диаграмму заданной пары металл-полупроводник в выбранном масштабе для случаев: без смещения, при прямом и обратном смещениях. Рассчитать вольтамперную характеристику контакта в данном диапазоне температур.
+
+## 7.1) Энергетическая диаграмма
+
+
+
+Вывод: в примесном полупроводнике энергия Ферми и работа выхода меньше,
+чем в собственном, но в обоих случаях растут по мере возрастания
+температуры.
+
+#
+
+# 7) Построить энергетическую диаграмму заданной пары металл-полупроводник в выбранном масштабе для случаев: без смещения, при прямом и обратном смещениях. Рассчитать вольтамперную характеристику контакта в данном диапазоне температур.
+
+## 7.1) Энергетическая диаграмма
+
+![]() +
+Рис. 24 Энергетическая диаграмма металл-вакуум-полупроводник
+
+
+
+Рис. 24 Энергетическая диаграмма металл-вакуум-полупроводник
+
+![]() +
+Рис. 25 Энергетическая диаграмма металл-полупроводник
+
+Вывод: Так как
+
+Рис. 25 Энергетическая диаграмма металл-полупроводник
+
+Вывод: Так как ![]() , следовательно, наблюдается
+анти-барьер Шоттки, или омический контакт.
+
+## 7.2) Вольт-амперная характеристика
+
+В ходе построений было вычислено, что работа выхода из примесного
+полупроводника
, следовательно, наблюдается
+анти-барьер Шоттки, или омический контакт.
+
+## 7.2) Вольт-амперная характеристика
+
+В ходе построений было вычислено, что работа выхода из примесного
+полупроводника ![]() , энергия контактной разности
+потенциалов
, энергия контактной разности
+потенциалов ![]() .
+
+Тогда, согласно уравнению Ричардсона, плотность тока
.
+
+Тогда, согласно уравнению Ричардсона, плотность тока ![]() .
+
+Где
.
+
+Где ![]() - плотность тока насыщения.
+
+Для трёх температур на рис. 28-30 приведены графики ВАХ.
+
+
- плотность тока насыщения.
+
+Для трёх температур на рис. 28-30 приведены графики ВАХ.
+
+![]() +
+Рис. 28 ВАХ контакта при *T* = 300 *К*
+
+
+
+Рис. 28 ВАХ контакта при *T* = 300 *К*
+
+![]() +
+Рис. 29 ВАХ контакта при *T* = 250 *К*
+
+
+
+Рис. 29 ВАХ контакта при *T* = 250 *К*
+
+![]() +
+Рис. 30 ВАХ контакта при *T* = 50 *К*
+
+Вывод: анти-барьер Шоттки виден и на ВАХ, где в области небольших напряжений выполняется
+закон Ома. Сопротивление в ней определяется только сопротивлением приконтактной области полупроводника.
+
+
+
+# 8) Рассчитать концентрацию носителей заряда в заданном полупроводнике для создания омического контакта к металлу.
+
+Как видно из п. 7, контакт Au-InSb образует анти-барьер Шоттки, поэтому
+дополнительно легированный буферный слой не требуется.
+
+# 9) Сделать выводы и дать рекомендации по применению исследуемого контакта металл-полупроводник
+
+В работе были исследованы металл золото (Au) и полупроводник антимонид
+индия (InSb). Оба материала имеют гранецентрированную кристаллическую
+решётку, характеристики каждой были исследованы в п. 1.
+
+В п. 2 на основании вычисления концентрации свободных электронов было
+выяснено, что к металлу неприменима теория свободных электронов.
+
+Золото является хорошим проводником, что было подтверждено в п. 3, где
+была исследована температурная зависимость проводимости и связанные с
+ней характеристики и влияние на неё дефектов кристаллической решётки.
+
+При этом, как показано в п. 4, при толщине менее 60 нм начинает
+сказываться размерный эффект — при отражении на неровностях теряется
+импульс по направлению движения электронов, из-за чего сильно возрастает
+сопротивление.
+
+В п. 5 на основании заданных эффективных масс электронов и «дырок» было
+выяснено, что антимонид индия является вырожденным, а значит, должно
+использоваться распределение Ферми-Дирака. Однако, далее в расчётах
+использовались формулы для невырожденного случая. В собственном
+полупроводнике, действительно, концентрации электронов и «дырок»
+совпали.
+
+С добавлением донорной примеси теллура (Te) при низких температурах
+концентрация электронов возрастает за счёт ионизации примесей, однако,
+по мере роста температуры они истощаются и уже при 366 К их вклад
+становится пренебрежимо мал. Проводимость полупроводника на несколько
+порядков меньше, чем у металла и возрастает по мере роста температуры.
+
+В п. 6 было показано, что добавление примеси в полупроводник уменьшает
+работу выхода.
+
+На основании энергетических диаграмм, построенных в п. 7 было выяснено,
+что золото и антимонид индия, легированных теллуром образуют омический
+контакт с высотой барьера
+
+Рис. 30 ВАХ контакта при *T* = 50 *К*
+
+Вывод: анти-барьер Шоттки виден и на ВАХ, где в области небольших напряжений выполняется
+закон Ома. Сопротивление в ней определяется только сопротивлением приконтактной области полупроводника.
+
+
+
+# 8) Рассчитать концентрацию носителей заряда в заданном полупроводнике для создания омического контакта к металлу.
+
+Как видно из п. 7, контакт Au-InSb образует анти-барьер Шоттки, поэтому
+дополнительно легированный буферный слой не требуется.
+
+# 9) Сделать выводы и дать рекомендации по применению исследуемого контакта металл-полупроводник
+
+В работе были исследованы металл золото (Au) и полупроводник антимонид
+индия (InSb). Оба материала имеют гранецентрированную кристаллическую
+решётку, характеристики каждой были исследованы в п. 1.
+
+В п. 2 на основании вычисления концентрации свободных электронов было
+выяснено, что к металлу неприменима теория свободных электронов.
+
+Золото является хорошим проводником, что было подтверждено в п. 3, где
+была исследована температурная зависимость проводимости и связанные с
+ней характеристики и влияние на неё дефектов кристаллической решётки.
+
+При этом, как показано в п. 4, при толщине менее 60 нм начинает
+сказываться размерный эффект — при отражении на неровностях теряется
+импульс по направлению движения электронов, из-за чего сильно возрастает
+сопротивление.
+
+В п. 5 на основании заданных эффективных масс электронов и «дырок» было
+выяснено, что антимонид индия является вырожденным, а значит, должно
+использоваться распределение Ферми-Дирака. Однако, далее в расчётах
+использовались формулы для невырожденного случая. В собственном
+полупроводнике, действительно, концентрации электронов и «дырок»
+совпали.
+
+С добавлением донорной примеси теллура (Te) при низких температурах
+концентрация электронов возрастает за счёт ионизации примесей, однако,
+по мере роста температуры они истощаются и уже при 366 К их вклад
+становится пренебрежимо мал. Проводимость полупроводника на несколько
+порядков меньше, чем у металла и возрастает по мере роста температуры.
+
+В п. 6 было показано, что добавление примеси в полупроводник уменьшает
+работу выхода.
+
+На основании энергетических диаграмм, построенных в п. 7 было выяснено,
+что золото и антимонид индия, легированных теллуром образуют омический
+контакт с высотой барьера ![]() и энергией сродства
+полупроводника
и энергией сродства
+полупроводника ![]() . Поэтому на вольт-амперной
+характеристике при небольших напряжениях наблюдается прямой участок,
+подчиняющийся закону Ома. При этом, так как с ростом напряжении при
+прямом включении наблюдается значительный рост тока, а при обратном
+«запирание» диода.
+
+Таким образом, полученный контакт можно использовать для соединения
+полупроводниковых приборов с металлическими выводами. Его удельное
+сопротивление получается порядка 10-14 Ом. Однако, уже при
+напряжениях порядка сотых долей вольта контакт становится выпрямляющим.
+
+# Список литературы
+
+1. Ситникова М.В. Методические указания к решению задач на практических
+ занятиях по дисциплине «Основы электроники и радиоматериалы»,
+ СпбГЭТУ «ЛЭТИ», 2021
+
+2. Астанин В.В. Электронное строение и кристаллическая структура
+ твердых тел. Учебное пособие. / Уфа: УГАТУ, 2007,- 132с.
+
+3. Ашкрофт Н., Мермин Н. Физика твердого тела. Т.1. М.: Мир, 1979
+
+4. Гольдберг Ю.А. Омический контакт металл--полупроводник AIIIBV:
+ методы создания и свойства // Физика и техника полупроводников.
+ 1994, вып (№) 10. С. 1681-1689
+
+32
. Поэтому на вольт-амперной
+характеристике при небольших напряжениях наблюдается прямой участок,
+подчиняющийся закону Ома. При этом, так как с ростом напряжении при
+прямом включении наблюдается значительный рост тока, а при обратном
+«запирание» диода.
+
+Таким образом, полученный контакт можно использовать для соединения
+полупроводниковых приборов с металлическими выводами. Его удельное
+сопротивление получается порядка 10-14 Ом. Однако, уже при
+напряжениях порядка сотых долей вольта контакт становится выпрямляющим.
+
+# Список литературы
+
+1. Ситникова М.В. Методические указания к решению задач на практических
+ занятиях по дисциплине «Основы электроники и радиоматериалы»,
+ СпбГЭТУ «ЛЭТИ», 2021
+
+2. Астанин В.В. Электронное строение и кристаллическая структура
+ твердых тел. Учебное пособие. / Уфа: УГАТУ, 2007,- 132с.
+
+3. Ашкрофт Н., Мермин Н. Физика твердого тела. Т.1. М.: Мир, 1979
+
+4. Гольдберг Ю.А. Омический контакт металл--полупроводник AIIIBV:
+ методы создания и свойства // Физика и техника полупроводников.
+ 1994, вып (№) 10. С. 1681-1689
+
+32
 -
- -
- -
- -
-![]() -,
-
-,
-![]() -,
-
-,
-![]() -
-![]() -
-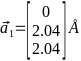 -,
-
-,
-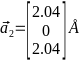 -,
-
-,
-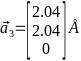 -
- -
-![]() -
-![]() -;
-
-;
-![]() -
-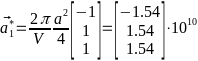 -,
-
-,
-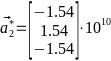 -,
-
-,
-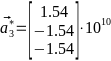 -
- -
- -
-![]() -
--
-центр верхнего квадрата, по направлению
-[001]
-
--
-центр верхнего квадрата, по направлению
-[001]![]() -
--
-центр шестиугольника, по направлению
-[111]
-
--
-центр шестиугольника, по направлению
-[111]![]() -
--
-середина грани соединяющей два
-шестиугольника, по направлению [101]
-
--
-середина грани соединяющей два
-шестиугольника, по направлению [101] -
-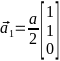 -,
-
-,
-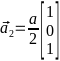 -,
-
-,
-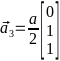 -,
-считая, что постоянная решётки = 1
-,
-считая, что постоянная решётки = 1![]() -
-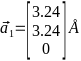 -,
-
-,
-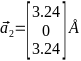 -,
-
-,
-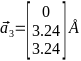 -
-![]() -
-![]() -;
-
-;
-![]() -
-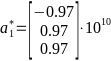 -,
-
-,
-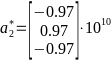 -,
-
-,
-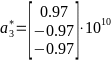 -
-![]() -.
-С другой стороны
-введено условие
-касания сферы Ферми с границей зоны
-Бриллюэна. Из п. 1 известно, что наименьшие
-размеры она имеет по направлению
-
-.
-С другой стороны
-введено условие
-касания сферы Ферми с границей зоны
-Бриллюэна. Из п. 1 известно, что наименьшие
-размеры она имеет по направлению
-![]() -,
-следовательно радиус
-Ферми для вписанной сферы
-
-,
-следовательно радиус
-Ферми для вписанной сферы
-![]() -
-![]() -
-![]() -,
-где Z — его валентность, N — количество
-атомов в его элементарной ячейке, а V —
-её объём.
-,
-где Z — его валентность, N — количество
-атомов в его элементарной ячейке, а V —
-её объём. -
-![]() -
-![]() -
-![]() -
-- наиболее частая
-
-- наиболее частая![]() -
-для любой возможной валентности,
-следовательно, теория свободных
-электронов не применима. Тогда эффективную
-массу электрона примем равной массе
-свободного электрона
-
-
-для любой возможной валентности,
-следовательно, теория свободных
-электронов не применима. Тогда эффективную
-массу электрона примем равной массе
-свободного электрона
-![]() -
-кг. В сравнении со стандартным металлом
-Пиппарда, у которого плотность электронов
-
-
-кг. В сравнении со стандартным металлом
-Пиппарда, у которого плотность электронов
-![]() -,
-а радиус Ферми
-
-,
-а радиус Ферми
-![]() -,
-у золота они получаются большими
-
-,
-у золота они получаются большими
-![]() -,
-
-,
-![]() -.
-.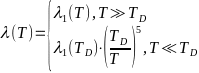 -.
-.![]() -,
-
-,
-![]() -
-— параметр решётки,
-
-
-— параметр решётки,
-![]() -
-— температура плавления
-
-
-— температура плавления
-![]() -
-— температура Дебая.
-
-— температура Дебая.![]() -,
-
-,
-![]() -,
-
-,
-![]() -
- -
-![]() -
-![]() -,
-где
-
-,
-где
-![]() -
-—
-скорость
-электронов на поверхности Ферми. В
-последней формуле
-
-
-—
-скорость
-электронов на поверхности Ферми. В
-последней формуле
-![]() -
-— постоянная
-Планка,
-
-
-— постоянная
-Планка,
-![]() -
-— концентрация носителей
-заряда,
-
-
-— концентрация носителей
-заряда,
-![]() -
-—
-эффективная масса электрона.
-
-—
-эффективная масса электрона.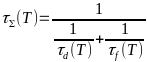 -.
-.![]() -;
-
-;
-![]() -;
-
-;
-![]() -
-![]() -,
-где
-
-,
-где
-![]() -
-— заряд электрона,
-
-
-— заряд электрона,
-![]() -
-— удельное
-сопротивление золота при Н.У.
-
-
-— удельное
-сопротивление золота при Н.У.
-![]() -.
-.![]() -.
-.![]() -,
-у
-золота она
-выше:
-
-
-,
-у
-золота она
-выше:
-
-![]() -.
-. -
-![]() -
-![]() -,
-где
-
-,
-где
-![]() -
-—
-число
-Лоренца, в
-чьей формуле присутствует
-
-
-—
-число
-Лоренца, в
-чьей формуле присутствует
-![]() -
-— постоянная Больцмана,
-а
-
-
-— постоянная Больцмана,
-а
-![]() -
-— электропроводность,
-выраженная через время релаксации из
-предыдущего подпункта.
-
-— электропроводность,
-выраженная через время релаксации из
-предыдущего подпункта.![]() -
-![]() -
- -
-![]() -
- -
-![]() -
- -
-![]() -
- -
-![]() -
-![]() -)
-температурные
-зависимости электропроводности
-и теплопроводности
-«выпрямляются»,
-вместе с чем также
-уменьшается их
-значение в каждой точке.
-При этом, с
-ростом температуры
-электропроводность
-убывает, а теплопроводность
-возрастает.
-)
-температурные
-зависимости электропроводности
-и теплопроводности
-«выпрямляются»,
-вместе с чем также
-уменьшается их
-значение в каждой точке.
-При этом, с
-ростом температуры
-электропроводность
-убывает, а теплопроводность
-возрастает.![]() -.
-Тогда количество дефектов в металле
-
-.
-Тогда количество дефектов в металле
-![]() -.
-
-
-.
-
-![]() -,
-количество
-дефектов
-меньше
-на
-10
-порядков, что можно
-назвать приемлемым значением.
-,
-количество
-дефектов
-меньше
-на
-10
-порядков, что можно
-назвать приемлемым значением.![]() -
-будут построены для двух значений
-параметра зеркальности p1 = 0
-и p2 = 0.5 в диапазоне температур
-
-
-будут построены для двух значений
-параметра зеркальности p1 = 0
-и p2 = 0.5 в диапазоне температур
-![]() -.
-.![]() -.
-Удельное сопротивление объёмного
-образца
-
-.
-Удельное сопротивление объёмного
-образца
-![]() -.
-.![]() -.
-Аналогично, для «тонкой плёнки»
-
-.
-Аналогично, для «тонкой плёнки»
-![]() -:
-
-:
-![]() -,
-где
-
-,
-где
-![]() -
- -
- -
-![]() -,
-что при заданном масштабе
-
-,
-что при заданном масштабе
-![]() -
-практически сольётся с
-
-
-практически сольётся с
-![]() -.
-Для данного металла это будет
-
-.
-Для данного металла это будет
-![]() -.
-Тогда толщина
-
-.
-Тогда толщина
-![]() -
-![]() -
-плёнка из золота должна демонстрировать
-металлические свойства. При этом, при
-большем коэффициенте зеркальности
-поверхности, действительно, удельное
-сопротивление по мере уменьшения толщины
-плёнки возрастает в меньшей степени.
-
-плёнка из золота должна демонстрировать
-металлические свойства. При этом, при
-большем коэффициенте зеркальности
-поверхности, действительно, удельное
-сопротивление по мере уменьшения толщины
-плёнки возрастает в меньшей степени.![]() -
-и
-
-
-и
-![]() -.
-.![]() -,
-где
-
-,
-где
-![]() -
-— ширина запрещённой зоны. (отсчёт идёт
-от потолка валентной зоны (EC).
-Соответствующее выражение для тепловой
-энергии:
-
-
-— ширина запрещённой зоны. (отсчёт идёт
-от потолка валентной зоны (EC).
-Соответствующее выражение для тепловой
-энергии:
-![]() -.
-Их график представлен на рис. 17.
-.
-Их график представлен на рис. 17. -
-![]() -
-выполняется для всех рассматриваемых
-температур, следовательно в этих
-условиях, электронный газ является
-вырожденным. Это значит, что он описывается
-распределением Ферми-Дирака:
-
-
-выполняется для всех рассматриваемых
-температур, следовательно в этих
-условиях, электронный газ является
-вырожденным. Это значит, что он описывается
-распределением Ферми-Дирака:
-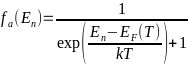 -.
-Например, для
-
-.
-Например, для
-![]() -,
-распределение показано на рис. 18.
-,
-распределение показано на рис. 18. -
-![]() -
-![]() -
-![]() -
- -
-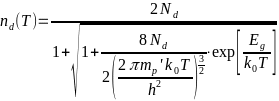 -
-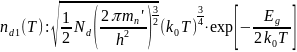 -
-![]() -
-![]() -
- -
- -
-![]() -,
-
-,
-![]() -,
-где
-
-,
-где
-![]() -
-и
-
-
-и
-![]() -
-— подвижности при 300 К.
-
-— подвижности при 300 К. -
-![]() -,
-где p(T) — концентрация дырок из
-подпункта 5.3, а n(T) — суммарная
-концентрация электронов из 5.4. График
-приведён на рис. 23
-,
-где p(T) — концентрация дырок из
-подпункта 5.3, а n(T) — суммарная
-концентрация электронов из 5.4. График
-приведён на рис. 23 -
-![]() -,
-где EF(T) — энергия Ферми
-из п. 5.2,
-
-,
-где EF(T) — энергия Ферми
-из п. 5.2,
-![]() -
-- энергия сродства
-
-- энергия сродства![]() -;
-
-;
-![]() -
-![]() -;
-
-;
-![]() -
-![]() -;
-
-;
-![]() -
-![]() -
-и
-
-
-и
-![]() -,
-,![]() -
-![]() -;
-
-;
-![]() -
-![]() -;
-
-;
-![]() -
-![]() -;
-
-;
-![]() -
- -
- -
-![]() -,
-следовательно, наблюдается анти-барьер
-Шоттки, или омический контакт.
-,
-следовательно, наблюдается анти-барьер
-Шоттки, или омический контакт.![]() -,
-энергия контактной разности потенциалов
-
-
-,
-энергия контактной разности потенциалов
-
-![]() -.
-.![]() -.
-.![]() -
-- плотность тока насыщения.
-
-- плотность тока насыщения. -
- -
- -
-![]() -
-и энергией сродства полупроводника
-
-
-и энергией сродства полупроводника
-![]() -.
-Поэтому на вольт-амперной характеристике
-при небольших напряжениях наблюдается
-прямой участок, подчиняющийся закону
-Ома. При этом, так как с ростом напряжении
-при прямом включении наблюдается
-значительный рост тока, а при обратном
-«запирание» диода.
-.
-Поэтому на вольт-амперной характеристике
-при небольших напряжениях наблюдается
-прямой участок, подчиняющийся закону
-Ома. При этом, так как с ростом напряжении
-при прямом включении наблюдается
-значительный рост тока, а при обратном
-«запирание» диода.